
����Ŀ����ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C���㣮
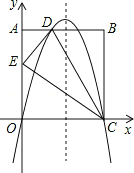
��1����AD�ij��������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ���������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
���𰸡���1��AD=3��![]() ��2����
��2����![]() ��
��![]() ʱ����P��Q��CΪ���������������ADE���ƣ�3�����ڷ���������M��N�㣬���ǵ�����Ϊ����M1����4����32����N1��4����38����
ʱ����P��Q��CΪ���������������ADE���ƣ�3�����ڷ���������M��N�㣬���ǵ�����Ϊ����M1����4����32����N1��4����38����
��M2��12����32����N2��4����26������M3��4��![]() ����N3��4����
����N3��4����![]() ��
��
��������
�⣺��1�����ı���ABCOΪ���Σ����OAB=��AOC=��B=90����AB=CO=8��AO=BC=10��
���۵������ʵã���BDC�ա�EDC�����B=��DEC=90����EC=BC=10��ED=BD��
�ɹ��ɶ�����EO=6����AE=10��6=4��
��AD=x����BD=CD=8��x���ɹ��ɶ�������x2+42=��8��x��2����ã�x=3��
��AD=3��
��������y=ax2+bx+c����D��3��10����C��8��0����
��![]() �����
�����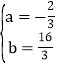 ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ��![]() ��
��
��2���ߡ�DEA+��OEC=90������OCE+��OEC=90�������DEA=��OCE��
�ɣ�1���ɵ�AD=3��AE=4��DE=5����CQ=t��EP=2t����PC=10��2t��
����PQC=��DAE=90������ADE�ס�QPC��
��![]() ����
����![]() �����
�����![]() ��
��
����QPC=��DAE=90������ADE�ס�PQC��
��![]() ����
����![]() �����
�����![]() ��
��
����![]() ��
��![]() ʱ����P��Q��CΪ���������������ADE���ơ�
ʱ����P��Q��CΪ���������������ADE���ơ�
��3�����ڷ���������M��N�㣬���ǵ�����Ϊ����M1����4����32����N1��4����38����
��M2��12����32����N2��4����26������M3��4��![]() ����N3��4����
����N3��4����![]() ����
����
��1�������۵�ͼ�ε���Գ��ԣ���CED�ա�CBD����Rt��CEO�����OE�ij����Ӷ��ɵõ�AE�ij�����Rt��AED�У�AD=AB��BD��ED=BD�����ù��ɶ��������AD�ij�����һ����ȷ��D�����꣬���ô���ϵ����������������ߵĽ���ʽ��
��2��������DEC=90����������ȷ��������AED=��OCE������P��Q��CΪ���������������ADE���ƣ���ô��QPC=90������PQC=90����Ȼ��������������£��ֱ��������������εĶ�Ӧ�߳ɱ��������Ӧ��t��ֵ��
��3��������ڷ���������M��N�㣬������������ۣ�
��ECΪƽ���ı��εĶԽ��ߣ����������ߵĶԳ��ᾭ��EC�е㣬���ı���MENC��ƽ���ı��Σ���ôM���Ϊ�����߶��㡣
��![]() �������߶��㣬��M��4��
�������߶��㣬��M��4��![]() ����
����
��ƽ���ı��εĶԽ�����ƽ�֣����߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4����![]() ����
����
��ECΪƽ���ı��εıߣ���EC![]() MN��
MN��
��N��4��m������M��4��8��m+6����M��4+8��m��6����
��M����4��m+6�����������ߵĽ���ʽ�У��ã�m=��38��
��ʱ N��4����38����M����4����32����
��M��12��m��6�����������ߵĽ���ʽ�У��ã�m=��26��
��ʱ N��4����26����M��12����32����
�������������ڷ���������M��N�㣬���ǵ�����Ϊ����M1����4����32����N1��4����38����
��M2��12����32����N2��4����26������M3��4��![]() ����N3��4����
����N3��4����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�![]() ��
��![]() ��ֱ��
��ֱ��![]() ��һ���㣬��
��һ���㣬��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬�����и�ֵ�����߶�
���е㣬�����и�ֵ�����߶�![]() �ij�����
�ij�����![]() ���ܳ�����
���ܳ�����![]() ���������ֱ��
���������ֱ��![]() ��
��![]() ֮��ľ��룻��
֮��ľ��룻��![]() �Ĵ�С�����в������
�Ĵ�С�����в������![]() ���ƶ����ı����_____��������ţ�
���ƶ����ı����_____��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
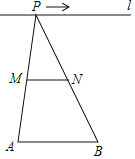
����Ŀ����ͼ��������![]() �У�
�У�![]() �ǶԽ���
�ǶԽ���![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() �ֱ�Ϊ���㣮
�ֱ�Ϊ���㣮
��1����֤��![]() ��
��
��2�����![]() ��
��![]() ��
��![]() �����߶�����ĵ�����ϵ����֤��������
�����߶�����ĵ�����ϵ����֤��������![]() ��
��![]() ʱ��
ʱ��![]() �ij�
�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˷ֱ�ӹ�100���������1��Сʱ�ӹ���10�������֮��ÿСʱ�ӹ�30����������ڼӹ�ǰ�Ѿ��ӹ���40��������ڼӹ�3Сʱ���ҿ�ʼ�ϼף��������ͬʱ���������ס������˸��Լӹ��������Ϊ![]() ���������ӹ������ʱ��Ϊ
���������ӹ������ʱ��Ϊ![]() ��ʱ����
��ʱ����![]() ��
��![]() ֮��ĺ���ͼ����ͼ��ʾ��
֮��ĺ���ͼ����ͼ��ʾ��

��1�������ϼĹ����У�����ÿСʱ�ӹ�����ĸ�����
��2�������ӹ��ٶȺ�ӹ��������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3�����ס����������12�����ʱ��ֱ��д���ӹ������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
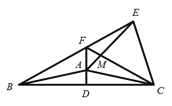
����Ŀ����֪����ͼ���ڵ���������ABC�У�120BAC180��ABAC��ADBC�ڵ�D����ACΪ�����ȱ�������ACE��ACE��ABC��ֱ��AC����ֱ࣬��BE��ֱ��AD�ڵ�F������FC��AE�ڵ�M��
��1����EFC�Ķ�����
��2����֤��FE+FA=FC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ĸ������ԼΪ700km���ס������˴����ݳ������ֱ���������ݺ�������A�������˺�������Bǰ����������֪A����ƽ���ٶȱ�B����ƽ���ٶ���80km/h��A������ʻʱ���B������ʻʱ���40%����������ʻʱ��ֱ�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
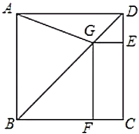
����Ŀ����ͼ������ABCD�У���ABD����CDB��ƽ����BE��DF�ֱ�AD��BC�ڵ�E��F��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2������ABEΪ���ٶ�ʱ���ı���BEDF�����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ����
����![]() ������
������![]() ��һ���㣬��
��һ���㣬��![]() Ϊ�����Ҳ����ȱ�
Ϊ�����Ҳ����ȱ�![]() ����
����![]() ��λ�����ŵ�
��λ�����ŵ�![]() ��λ�ñ仯���仯.
��λ�ñ仯���仯.
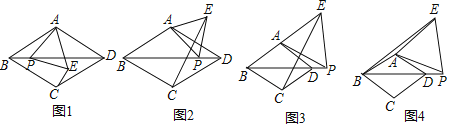
��1����ͼ1������![]() ������
������![]() �ڲ������ʱ������
�ڲ������ʱ������![]() ��
��![]() ��
��![]() ��������ϵ��______��
��������ϵ��______��![]() ��
��![]() ��λ�ù�ϵ��______��
��λ�ù�ϵ��______��
��2������![]() ������
������![]() �ⲿʱ����1���еĽ����Ƿ�������������������֤����������������˵�����ɣ�ѡ��ͼ2��ͼ3�е�һ���������֤����˵������
�ⲿʱ����1���еĽ����Ƿ�������������������֤����������������˵�����ɣ�ѡ��ͼ2��ͼ3�е�һ���������֤����˵������
��3����ͼ4������![]() ���߶�
���߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ����
����![]() ��
��![]() �����ı���
�����ı���![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() Ϊ���Σ���֪
Ϊ���Σ���֪![]() ��
��![]() ��
��
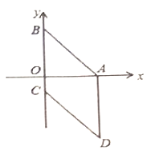
��1�����![]() �����ꣻ
�����ꣻ
��2������![]() ��
��![]() �����һ�κ����Ľ���ʽ��
�����һ�κ����Ľ���ʽ��
��3��������![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com