
����Ŀ��������![]() �У�
��![]() ����
����![]() ������
������![]() ��һ���㣬��
��һ���㣬��![]() Ϊ�����Ҳ����ȱ�
Ϊ�����Ҳ����ȱ�![]() ����
����![]() ��λ�����ŵ�
��λ�����ŵ�![]() ��λ�ñ仯���仯.
��λ�ñ仯���仯.
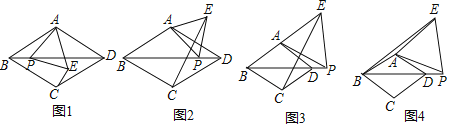
��1����ͼ1������![]() ������
������![]() �ڲ������ʱ������
�ڲ������ʱ������![]() ��
��![]() ��
��![]() ��������ϵ��______��
��������ϵ��______��![]() ��
��![]() ��λ�ù�ϵ��______��
��λ�ù�ϵ��______��
��2������![]() ������
������![]() �ⲿʱ����1���еĽ����Ƿ�������������������֤����������������˵�����ɣ�ѡ��ͼ2��ͼ3�е�һ���������֤����˵������
�ⲿʱ����1���еĽ����Ƿ�������������������֤����������������˵�����ɣ�ѡ��ͼ2��ͼ3�е�һ���������֤����˵������
��3����ͼ4������![]() ���߶�
���߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ����
����![]() ��
��![]() �����ı���
�����ı���![]() �����.
�����.
���𰸡���1��![]() ��
��![]() ����2��������Ȼ���������ɣ��ԣ���3��
����2��������Ȼ���������ɣ��ԣ���3��![]()
��������
��1������AC���������ε����ʺ͵ȱ������ε����ʵó���BAP�ա�CAE�����ӳ�![]() ��
��![]() ��
��![]() �� ����ȫ�������ε����ʼ��ɵó���
�� ����ȫ�������ε����ʼ��ɵó���
��2��������Ȼ������֤������ͬ��1����
��3�����ݣ�2����֪��BAP�ա�CAE�����ݹ��ɶ����ֱ����AP��EC�ij���![]() ���ɽ�����⣻
���ɽ�����⣻
��1����ͼ1�У����ۣ�![]() ��
��![]() .
.
���ɣ�����![]() .
.
���ı���![]() �����Σ�
������![]() ��
��
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�![]() ��
��
��![]() ��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
 ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
�ӳ�![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() .
.
�ʴ�Ϊ![]() ��
��![]() .
.
��2��������Ȼ����.
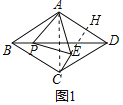
���ɣ�ѡͼ2������![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() .
.

���ı���![]() �����Σ�
������![]() ��
��
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�![]() ��
��
��![]() ��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]() .
.
 ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() .
.
ѡͼ3������![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() .
.
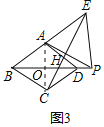
���ı���ABCD�����Σ�![]() ��
��
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]() .
.
 ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() .
.
��3��![]() ��
��
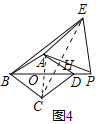
�ɣ�2����֪![]() ��
��![]() ��
��
������![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �����εĶԽ��ߣ�
�����εĶԽ��ߣ�
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]()
![]() .
.


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
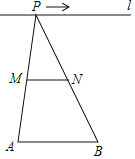
����Ŀ����ͼ����֪�߶�![]() ��
��![]() ��ֱ��
��ֱ��![]() ��һ���㣬��
��һ���㣬��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬�����и�ֵ�����߶�
���е㣬�����и�ֵ�����߶�![]() �ij�����
�ij�����![]() ���ܳ�����
���ܳ�����![]() ���������ֱ��
���������ֱ��![]() ��
��![]() ֮��ľ��룻��
֮��ľ��룻��![]() �Ĵ�С�����в������
�Ĵ�С�����в������![]() ���ƶ����ı����_____��������ţ�
���ƶ����ı����_____��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C���㣮
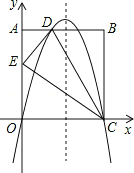
��1����AD�ij��������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ���������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���BAC=90![]() ��AB=AC.��DΪֱ��BC��һ���㣨��D�����B��C�غϣ�����ADΪֱ�DZ���AD�Ҳ�������ֱ��������ADE��ʹ
��AB=AC.��DΪֱ��BC��һ���㣨��D�����B��C�غϣ�����ADΪֱ�DZ���AD�Ҳ�������ֱ��������ADE��ʹ![]() DAE=90
DAE=90![]() ������CE.
������CE.
̽������ͼ�٣�����D���߶�BC��ʱ��֤��BC=CE+CD.
Ӧ�ã���̽���������£���AB=![]() ��CD=1������DCE���ܳ�Ϊ_______.
��CD=1������DCE���ܳ�Ϊ_______.
��չ��(1)��ͼ�ڣ�����D���߶�CB���ӳ�����ʱ��BC��CD��CE֮���������ϵΪ_______.
(2)��ͼ�ۣ�����D���߶�BC���ӳ�����ʱ��BC��CD��CE֮���������ϵΪ_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() ��������
��������![]() ��x���ཻ��A��B���㣬����A�������Ϊ����3��0����
��x���ཻ��A��B���㣬����A�������Ϊ����3��0����

��1�����B�����ꣻ
��2����֪![]() ��CΪ��������y��Ľ��㡣
��CΪ��������y��Ľ��㡣
������P���������ϣ���![]() �����P�����ꣻ
�����P�����ꣻ
�����Q���߶�AC�ϵĶ��㣬��QD��x�ύ�������ڵ�D�����߶�QD���ȵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��120�㣬OPƽ�֡�AOB����OP��1������M��N�ֱ���OA��OB�ϣ��ҡ�PMNΪ�ȱ������Σ����������������ġ�PMN��(����)
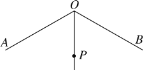
A.1��B.2��C.3��D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ�������
�ǵȱ�������![]() ��һ�㣬���߶�
��һ�㣬���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת60��õ��߶�
˳ʱ����ת60��õ��߶�![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �����Ϊ___________��
�����Ϊ___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ��� y��ax2+bx+c��a��0��������1��y1����2��y2����
���� y1��0 ʱ���� a+b+c��0
���� a��b ʱ���� y1��y2
���� y1��0��y2��0���� a+b��0���� a��0
���� b��2a��1��c��a��3���� y1��0���������ߵĶ���һ���ڵ������������ĸ��ж���ȷ���У� ������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
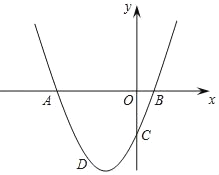
����Ŀ����֪��������y��ax2+2ax+c��y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ��1��0����OC��3OB��
��1���������ߵĽ���ʽ��
��2����a��0ʱ����ͼ��ʾ������D�ǵ��������������ϵĶ��㣬���D�ĺ�����Ϊm��������ADC�����ΪS�����S��m�ĺ�����ϵʽ����ֱ��д���Ա���m��ȡֵ��Χ�����ʵ�mΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com