
ЁОЬтФПЁПШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌЁЯDABБЛЖдНЧЯпACЦНЗжЃЌЧвAC2ЃНABADЃЌЮвУЧГЦИУЫФБпаЮЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABГЦЮЊЁАПЩЗжНЧЁБЃЎ
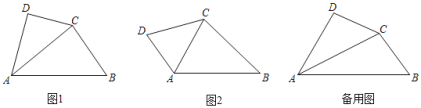
ЃЈ1ЃЉШчЭМ2ЃЌЫФБпаЮABCDЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABЮЊЁАПЩЗжНЧЁБЃЌЧѓжЄЃКЁїDACЁзЁїCABЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЫФБпаЮABCDЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABЮЊЁАПЩЗжНЧЁБЃЌШчЙћЁЯDCBЃНЁЯDABЃЌдђЁЯDABЃН Ёу
ЃЈ3ЃЉЯжгаЫФБпаЮABCDЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABЮЊЁАПЩЗжНЧЁБЃЌЧвACЃН4ЃЌBCЃН2ЃЌЁЯDЃН90ЁуЃЌЧѓADЕФГЄ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ120ЁуЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШХаЖЯГі![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩвбжЊЬѕМўПЩжЄЕУЁїADCЁзЁїACBЃЌЕУГіD=ЁЯ4ЃЌдйгЩвбжЊЬѕМўКЭШ§НЧаЮФкНЧКЭЖЈРэЕУГіЁЯ1+2ЁЯ1=180ЁуЃЌЧѓГіЁЯ1=60ЁуЃЌМДПЩЕУГіЁЯDABЕФЖШЪ§ЃЛ
ЃЈ3ЃЉгЩвбжЊЕУГіAC2=ABADЃЌЁЯDAC=ЁЯCABЃЌжЄГіЁїADCЁзЁїACBЃЌЕУГіЁЯD=ЁЯACB=90ЁуЃЌгЩЙДЙЩЖЈРэЧѓГіABЃЌМДПЩЕУГіADЕФГЄЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮABCDЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABЮЊЁАПЩЗжНЧЁБЃЌ
ЁрAC2ЃНABADЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯDABЮЊЁАПЩЗжНЧЁБЃЌ
ЁрЁЯCADЃНЁЯBACЃЌ
ЁрЁїDACЁзЁїCABЃЛ
ЃЈ2ЃЉНтЃКШчЭМЫљЪОЃК
ЁпACЦНЗжЁЯDABЃЌ
ЁрЁЯ1ЃНЁЯ2ЃЌ
ЁпAC2ЃНABADЃЌ
ЁрADЃКACЃНACЃКABЃЌ
ЁрЁїADCЁзЁїACBЃЌ
ЁрЁЯDЃНЁЯ4ЃЌ
ЁпЁЯDCBЃНЁЯDABЃЌ
ЁрЁЯDCBЃНЁЯ3+ЁЯ4ЃН2ЁЯ1ЃЌ
ЁпЁЯ1+ЁЯD+ЁЯ3ЃНЁЯ1+ЁЯ4+ЁЯ3ЃН180ЁуЃЌ
ЁрЁЯ1+2ЁЯ1ЃН180ЁуЃЌ
НтЕУЃКЁЯ1ЃН60ЁуЃЌ
ЁрЁЯDABЃН120ЁуЃЛ
ЙЪД№АИЮЊЃК120ЃЛ
ЃЈ3ЃЉНтЃКЁпЫФБпаЮABCDЮЊЁАПЩЗжЫФБпаЮЁБЃЌЁЯDABЮЊЁАПЩЗжНЧЁБЃЌ
ЁрAC2ЃНABADЃЌЁЯDACЃНЁЯCABЃЌ
ЁрADЃКACЃНACЃКABЃЌ
ЁрЁїADCЁзЁїACBЃЌ
ЁрЁЯDЃНЁЯACBЃН90ЁуЃЌ
ЁрABЃН![]() ЃЌ
ЃЌ
ЁрADЃН![]() .
.
ЙЪД№АИЮЊ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕФкЃЌвбжЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊЃЈ____ЃЌ______ЃЉЃЛ
ЃЈ2ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЖШ
ЖШ![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЧЁКУТфдкЗДБШР§КЏЪ§
ЧЁКУТфдкЗДБШР§КЏЪ§![]()
![]() ЕФЭМЯѓЩЯЃЌЧѓ
ЕФЭМЯѓЩЯЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
Ђкдка§зЊЙ§ГЬжаЃЌЕу![]() ФмЗёЭЌЪБТфдкЩЯЪіЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌШєФмЃЌЧѓГі
ФмЗёЭЌЪБТфдкЩЯЪіЗДБШР§КЏЪ§ЕФЭМЯѓЩЯЃЌШєФмЃЌЧѓГі![]() ЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
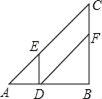
ЃЌ ![]() ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзї
ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзї![]() НЛBCБпгкЕуFЃЌСЊНсEFЃЎ
НЛBCБпгкЕуFЃЌСЊНсEFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() ЪБЃЌЧѓEFЕФГЄЃЛ
ЪБЃЌЧѓEFЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкACБпЩЯвЦЖЏЪБЃЌ ![]() ЕФе§ЧажЕЪЧЗёЛсЗЂЩњБфЛЏЃЌШчЙћБфЛЏЧыЫЕГіБфЛЏЧщПіЃЛШчЙћБЃГжВЛБфЃЌЧыЧѓГі
ЕФе§ЧажЕЪЧЗёЛсЗЂЩњБфЛЏЃЌШчЙћБфЛЏЧыЫЕГіБфЛЏЧщПіЃЛШчЙћБЃГжВЛБфЃЌЧыЧѓГі![]() ЕФе§ЧажЕЃЛ
ЕФе§ЧажЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌСЊНсCDНЛEFгкЕуQЃЌЕБ![]() ЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіBFЕФГЄЃЎ
ЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіBFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаПМЬхг§ВтЪдЧАЃЌФГЧјНЬг§ОжЮЊСЫСЫНтбЁБЈв§ЬхЯђЩЯЕФГѕШ§ФаЩњЕФГЩМЈЧщПіЃЌЫцЛњГщВтСЫБОЧјВПЗжбЁБЈв§ЬхЯђЩЯЯюФПЕФГѕШ§ФаЩњЕФГЩМЈЃЌВЂНЋВтЪдЕУЕНЕФГЩМЈЛцГЩСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃК

ЧыФуИљОнЭМжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЙШЋЬѕаЮЭМЃЛ
ЃЈ2ЃЉжБНгаДГідкетДЮГщВтжаЃЌВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉИУЧјЬхг§жаПМбЁБЈв§ЬхЯђЩЯЕФФаЩњЙВга1800ШЫЃЌШчЙћЬхг§жаПМв§ЬхЯђЩЯДя6ИівдЩЯ(КЌ6Иі)ЕУТњЗжЃЌЧыФуЙРМЦИУЧјЬхг§жаПМжабЁБЈв§ЬхЯђЩЯЕФФаЩњФмЛёЕУТњЗжЕФгаЖрЩйУћ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
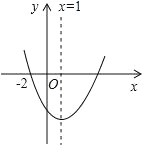
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЙ§ЃЈЉ2ЃЌ0ЃЉЃЌдђЯТСаНсТлЃКЂйbcЃО0Ђкb+2aЃН0ЃЛЂлa+cЃОbЃЛЂм16a+4b+cЃН0ЃЛЂн3a+cЃМ0ЃЌЦфжае§ШЗЕФНсТлЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
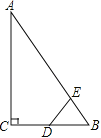
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃНBCЃН12cmЃЌЕуDДгЕуAПЊЪМбиБпABвд2cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌвЦЖЏЙ§ГЬжаЪМжеБЃГжDEЁЮBCЃЌDFЁЮACЃЌ
ЧѓЃКГіЗЂМИУыЪБЃЌЫФБпаЮDFCEЕФУцЛ§ЮЊ20cm2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯABC=60ЁуЃЌBC=2cmЃЌDЮЊBCЕФжаЕуЃЌШєЖЏЕуEвд1cm/sЕФЫйЖШДгAЕуГіЗЂЃЌбизХAЁњBЁњAЕФЗНЯђдЫЖЏЃЌЩшEЕуЕФдЫЖЏЪБМфЮЊtУыЃЈ0ЁмtЃМ6ЃЉЃЌСЌНгDEЃЌЕБЁїBDEЪЧжБНЧШ§НЧаЮЪБЃЌtЕФжЕЮЊ
AЁЂ2 BЁЂ2.5Лђ3.5 CЁЂ3.5Лђ4.5 DЁЂ2Лђ3.5Лђ4.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЧвЯрНЛгкСэвЛЕу
ЃЌЧвЯрНЛгкСэвЛЕу![]() ЃЌХзЮяЯпгы
ЃЌХзЮяЯпгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкСэвЛЕу
жсНЛгкСэвЛЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЕФжБЯпНЛХзЮяЯпгкЕу
ЕФжБЯпНЛХзЮяЯпгкЕу![]() ЃЌЧв
ЃЌЧв![]() жсЃЌСЌНг
жсЃЌСЌНг![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвЦЖЏЪБЃЈВЛгы
ЩЯвЦЖЏЪБЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
жиКЯЃЉЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A.![]() B.
B.![]()
C.![]() D.ЫФБпаЮ
D.ЫФБпаЮ![]() ЕФзюДѓУцЛ§ЮЊ13
ЕФзюДѓУцЛ§ЮЊ13
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
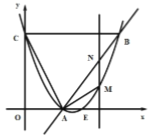
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌOЮЊзјБъдЕуЃЌЫФБпаЮOABCЮЊОиаЮЃЌBЃЈ5ЃЌ2ЃЉЃЌЕуDЪЧOAЕФжаЕуЃЌЖЏЕуPдкЯпЖЮBCЩЯвдУПУы2ИіЕЅЮЛГЄЕФЫйЖШгЩЕуCЯђB дЫЖЏЃЎЩшЖЏЕуPЕФдЫЖЏЪБМфЮЊtУы
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮPODBЪЧЦНааЫФБпаЮЃП
ЃЈ2ЃЉдкжБЯпCBЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУOЁЂDЁЂQЁЂPЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧѓtЕФжЕЃЌВЂЧѓГіQЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЯпЖЮPBЩЯгавЛЕуMЃЌЧвPMЃН2.5ЃЌЕБPдЫЖЏЖрЩйЃЌЫФБпаЮOAMPЕФжмГЄзюаЁжЕЮЊЖрЩйЃЌВЂЛЭМБъГіЕуMЕФЮЛжУЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com