练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

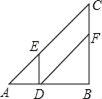
    【题目】如图，在Rt△ABC中，∠B＝90°，AB＝BC＝12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC，

    求：出发几秒时，四边形DFCE的面积为20cm2．

    【答案】出发1秒或5秒时，四边形DFCE的面积为20cm2．

    【解析】

    设点D从点A出发x秒时，则四边形DFCE的面积为20cm2．根据S四边形DECF=S△ABC-S△ADE-S△BDF，就可以求出结论．

    设点D从点A出发x秒时，则四边形DFCE的面积为20cm2，由题意，得

    ×12×12﹣×2x×2x﹣（12﹣2x）（12﹣2x）＝20，

    解得：x1＝1，x2＝5．

    答：出发1秒或5秒时，四边形DFCE的面积为20cm2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润．下列结论错误的是（　　）

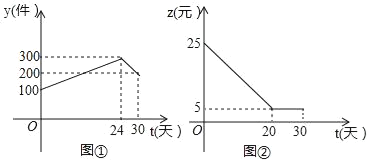
    A.第24天的销售量为300件

    B.第10天销售一件产品的利润是15元

    C.第27天的日销售利润是1250元

    D.第15天与第30天的日销售量相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

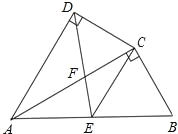
    【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，

    （1）求证：AC2＝ABAD；

    （2）求证：△AFD∽△CFE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“低碳生活，绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.

    （1）若1月份到4月份新投放单车数量的月平均增长率相同，3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆？

    （2）考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A，B两种规格的自行车100辆，已知A型的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆。假设所进车辆全部售完，为了使利润最大，该商城应如何进货？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在四边形ABCD中，∠DAB被对角线AC平分，且AC2＝ABAD，我们称该四边形为“可分四边形”，∠DAB称为“可分角”．

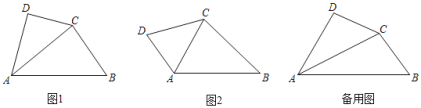
    （1）如图2，四边形ABCD为“可分四边形”，∠DAB为“可分角”，求证：△DAC∽△CAB．

    （2）如图2，四边形ABCD为“可分四边形”，∠DAB为“可分角”，如果∠DCB＝∠DAB，则∠DAB＝ °

    （3）现有四边形ABCD为“可分四边形”，∠DAB为“可分角”，且AC＝4，BC＝2，∠D＝90°，求AD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y＝﹣x2+bx+c经过点A、C，与AB交于点D．

    （1）求抛物线的函数解析式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．

    ①求S关于m的函数表达式；

    ②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个转盘（如图所示），被分成6个相等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，重新转动）．下列事件：①指针指向红色；②指针指向绿色；③指针指向黄色；④指针不指向黄色．估计各事件的可能性大小，完成下列问题：

    （1）可能性最大和最小的事件分别是哪个？（填写序号）

    （2）将这些事件的序号按发生的可能性从小到大的顺序排列： ．

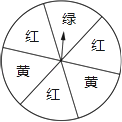
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．

    （1）当t为何值时，AD=AB，并求出此时DE的长度；

    （2）当△DEG与△ACB相似时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个布口袋里装着白、红、黑三种颜色的小球，它们除颜色之外没有任何其它区别，其中有白球3只、红球2只、黑球1只．袋中的球已经搅匀．

    （1）闭上眼睛随机地从袋中取出1只球，求取出的球是黑球的概率；

    （2）若取出的第1只球是红球，将它放在桌上，闭上眼睛从袋中余下的球中再随机地取出1只球，这时取出的球还是红球的概率是多少？

    （3）若取出一只球，将它放回袋中，闭上眼睛从袋中再随机地取出1只球，两次取出的球都是白球概率是多少？（用列表法或树状图法计算）

    查看答案和解析>>

    同步练习册答案