
【题目】在平面直角坐标系内,已知![]() .
.
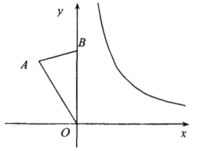
(1)点A的坐标为(____,______);
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() .
.
①当![]() 时,点
时,点![]() 恰好落在反比例函数
恰好落在反比例函数![]()
![]() 的图象上,求
的图象上,求![]() 的值;
的值;
②在旋转过程中,点![]() 能否同时落在上述反比例函数的图象上,若能,求出
能否同时落在上述反比例函数的图象上,若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)A(-1,![]() );(2)①
);(2)①![]() ;②
;②![]() ,理由见解析
,理由见解析
【解析】
(1)作AC⊥x轴于点C,在直角△AOC中,利用三角函数即可求得AC、OC的长度,则A的坐标即可求解;
(2)①当a=30时,点B的位置与A一定关于y轴对称,在B的坐标可以求得,利用待定系数法即可求得反比例函数的解析式;
②当![]() =60°时,旋转后点的横纵坐标正好互换,则一定都在反比例函数的图象上.
=60°时,旋转后点的横纵坐标正好互换,则一定都在反比例函数的图象上.
解:(1)作AC⊥x轴于点C,
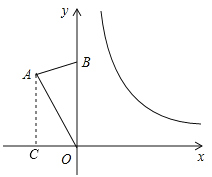
在直角△AOC中,∠AOC=90°-∠AOB=60°,
则AC=OAsin∠AOC=2×![]() =
=![]() ,OC=OAcos60°=2×
,OC=OAcos60°=2×![]() =1,
=1,
则A的坐标是(-1,![]() );
);
(2)①当![]() =30°时,B的坐标与A(-1,
=30°时,B的坐标与A(-1,![]() )一定关于y轴对称,
)一定关于y轴对称,
则旋转后的点B(1,![]() ).
).
把(1,![]() )代入函数解析式得:k=
)代入函数解析式得:k=![]() ;
;
②当![]() =60°时,旋转后点A(1,
=60°时,旋转后点A(1,![]() ),点B(
),点B(![]() ,1),
,1),
∵xy=![]() ,
,
∴当![]() =60°,A、B能同时落在上述反比例函数的图象上.
=60°,A、B能同时落在上述反比例函数的图象上.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
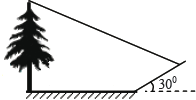
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面xOy中,二次函数y=x2+2(m+2)x+m﹣2图象与y轴交于(0,﹣3)点.
(1)求该二次函数的解析式,并画出示意图;
(2)将该二次函数图象向左平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD,AD∥BC,AD=2![]() ,BD=BC=3
,BD=BC=3![]() ,AC=4
,AC=4![]() ,将AC沿着AD方向平移至DE,使得点A与点D对应,点C与点E对应.
,将AC沿着AD方向平移至DE,使得点A与点D对应,点C与点E对应.
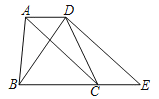
(1)猜想DE与BD的位置关系,并证明你的结论;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
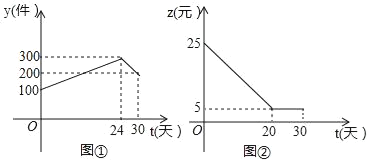
A.第24天的销售量为300件
B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元
D.第15天与第30天的日销售量相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
测试项目 | 测试成绩 | |
小文 | 小明 | |
应变能力 | 70 | 80 |
知识面 | 80 | 72 |
朗诵水平 | 87 | 85 |
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占![]() ,知识面占
,知识面占![]() ,其中
,其中![]() ,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的
,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以2cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以1cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是a秒(0<a≤20).过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的a值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
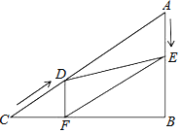
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
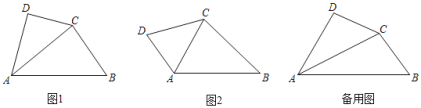
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.
(2)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB= °
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com