
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+8与x轴相交于点A(﹣2,0)和点B(4,0),与y轴相交于点C,顶点为点P.点D(0,4)在OC上,联结BC、BD.
(1)求抛物线的表达式并直接写出点P的坐标;
(2)点E为第一象限内抛物线上一点,如果△COE与△BCD的面积相等,求点E的坐标;
(3)点Q在抛物线对称轴上,如果△BCD∽△CPQ,求点Q的坐标.
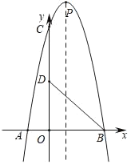
【答案】(1)点P的坐标为(1,9);(2)点E的坐标为(2,8);(3)点Q的坐标为(1,11)或(1,10).
【解析】
(1)通过待定系数法代入A、B坐标即可求得解析式;
(2)根据解析式可求得点C坐标(0,8),根据点E为第一象限内抛物线上一点设点E((x,﹣x2+2x+8)再根据S△COE=S△BCD,可求得E点坐标.
(3)根据点B、D的坐标可得到∠BDC=135°,要满足△BCD∽△CPQ,∠CPQ=135°或者∠PCQ=135°,通过点C、P的坐标可得,∠PCM=45°,所以∠MCQ=90°,Q在对称轴上,此情况不成立,所以要满足△BCD∽△CPQ,仅∠CPQ=135°,即Q在P点上方,可分两类讨论,![]() 或
或![]() 代值即可求出Q点坐标.
代值即可求出Q点坐标.
(1)将点A(﹣2,0),B(4,0)代入y=ax2+bx+8,得:
![]()
解得:![]() ,
,
∴抛物线的表达式为y=﹣x2+2x+8.
∵y=﹣x2+2x+8=﹣(x﹣1)2+9,
∴点P的坐标为(1,9).
(2)当x=0时,y=﹣x2+2x+8=8,
∴点C的坐标为(0,8).
设点E的坐标为(x,﹣x2+2x+8)(0<x<4),
∵S△COE=S△BCD,
∴![]() ×8x=
×8x=![]() ×4×4,
×4×4,
解得:x=2,
∴点E的坐标为(2,8).
(3)过点C作CM∥x轴,交抛物线对称轴于点M,如图所示.
∵点B(4,0),点D(0,4),
∴OB=OD=4,
∴∠ODB=45°,BD=4![]() ,
,
∴∠BDC=135°.
∵点C(0,8),点P(1,9),
∴点M的坐标为(1,8),
∴CM=PM=1,
∴∠CPM=45°,CP=![]() ,
,
∴点Q在抛物线对称轴上且在点P的上方,
∴∠CPQ=∠CDB=135°.
∵△BCD∽△CPQ,
∴![]() 或
或![]() .
.
①当![]() 时,
时,![]() ,
,
解得:PQ=2,
∴点Q的坐标为(1,11);
②当![]() 时,
时,![]() ,
,
解得:PQ=1,
∴点Q的坐标为(1,10).
综上所述,点Q的坐标为(1,11)或(1,10).



 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(2,0).OC=3OB.
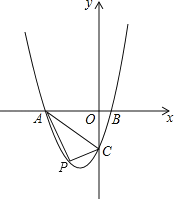
(1)求抛物线的解析式;
(2)若点P是线段AC下方抛物线上的动点,求三角形PAC面积的最大值.
(3)在(2)的条件下,△PAC的面积为S,其中S为整数的点P作“好点”,则存在多个“好点”,则所有“好点”的个数为
(4)在(2)的条件下,以PA为边向直线AC右上侧作正方形APHG,随着点P的运动,正方形的大小、位置也随之改变,当顶点H或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
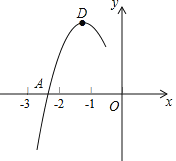
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现, 销售量y(件)与销售单价x(元)符合一次函数,所调查的部分数据如表:
销售单价x(元) | 65 | 70 | 80 | … |
销售量y(件) | 55 | 50 | 40 | … |
(1)求出y与x之间的函数表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少?
(3)销售单价定为多少元时,该商场获得的利润恰为500元?
查看答案和解析>>
科目:初中数学 来源: 题型:
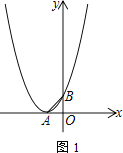
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
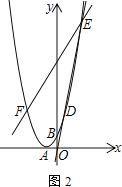
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+4与抛物线y=![]() x2交于点A(x1,y1),B(x2,y2).
x2交于点A(x1,y1),B(x2,y2).
(1)求:![]() ;
;![]() 的值.
的值.
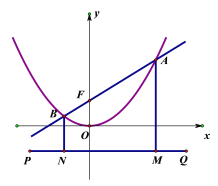
(2)过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.
(3)证明:![]() +
+![]() 为定值,并求出该值.
为定值,并求出该值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 先向左平移
先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到抛物线
个单位长度,得到抛物线![]() .
.
(1)试确定![]() 的值;
的值;
(2)作原抛物线关于![]() 轴对称的图形,求所得抛物线的函数表达式.
轴对称的图形,求所得抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B. D两点.
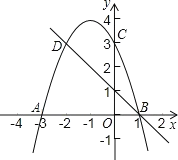
(1)求a、b的值及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译![]() 若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com