
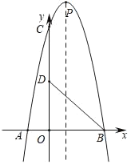
����Ŀ����֪����ͼ������y��ax2+3ax+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ��2��0����OC��3OB��
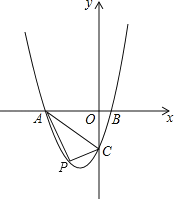
��1���������ߵĽ���ʽ��
��2������P���߶�AC�·��������ϵĶ��㣬��������PAC��������ֵ��
��3���ڣ�2���������£���PAC�����ΪS������SΪ�����ĵ�P�����õ���������ڶ�����õ��������������õ����ĸ���Ϊ�� ��
��4���ڣ�2���������£���PAΪ����ֱ��AC���ϲ���������APHG�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣬������H��Gǡ������y����ʱ��ֱ��д����Ӧ�ĵ�P�����꣮
���𰸡���1�������ߵı���ʽΪ��y��![]() x2+
x2+![]() x��6��
x��6��
��2����x����![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ��![]() ��
��
��3��4��
��4����P����������![]() ����5����
����5����![]() ��
��![]() ����
����
��������
��1����ȷ����C�����꣬�����ô���ϵ������⣻
��2�������ֱ��AC�Ľ���ʽ���ٹ���P��y���ƽ���߽�AC�ڵ�H�����P�ĺ�����Ϊx��������PAC���S��![]() PH��OA����OA����ֻ���ú�x�Ĵ���ʽ��ʾ��PH�ij��������ö��κ�����������������
PH��OA����OA����ֻ���ú�x�Ĵ���ʽ��ʾ��PH�ij��������ö��κ�����������������
��3�����ݣ�2����Ĺ�ϵʽ�����x�ķ�Χ��һ��֤S�Ƿ�Ϊ�������ô𰸣�
��4���ֵ�G��y���Ϻ͵�H��y����������������������ε����ʹ���ȫ�������ηֱ���⼴��.
�⣺��1��OC��3OB��6���ʵ�B��C������ֱ�Ϊ����2��0������0����6������������Ϊy��ax2+3ax��6��
����B�����������ʽ�ã�0��4a+6a��6����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2+
x2+![]() x��6��
x��6��
��2��y��![]() x2+
x2+![]() x��6����y��0����x����5��2���ʵ�A����5��0����
x��6����y��0����x����5��2���ʵ�A����5��0����
����A��C���������һ�κ�������ʽ��y��kx+b����ã�ֱ��AC�Ľ���ʽΪ��y����![]() x��6��
x��6��
����P��y���ƽ���߽�AC�ڵ�H��

���P��x��![]() x2+
x2+![]() x��6������H��x����
x��6������H��x����![]() x��6����
x��6����
��PAC���S��![]() PH��OA��
PH��OA��![]() ����
����![]() x2��
x2��![]() x
x![]() ��
��
�ߩ�![]() <0����S�����ֵ�� ��x����
<0����S�����ֵ�� ��x����![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ��![]() ��
��
��3����PAC���S����![]() x2��
x2��![]() x����Ϊ��P���߶�AC�·��������ϵĵ㣬���ԣ�5<x<0��
x����Ϊ��P���߶�AC�·��������ϵĵ㣬���ԣ�5<x<0��
��x����4ʱ��S��6����x����3ʱ��s��9����x����2ʱ��S=9����x����1ʱ��s��6��
���ԡ��õ㡱�ĸ���Ϊ4��
�ʴ�Ϊ4��
��4����ͼ2���ͼ��
������G��y����ʱ����PR��x���ڵ�R��
�ߡ�GAO+��PAO��90������PAO+��APR��90����
���APR����GAO��
�ߡ�AOG����PRA��90����AP��AG��
���AOG�ա�PRA��AAS����
��OA��PR��5��
�ʵ�P��������Ϊ����5��
��y��![]() x2+
x2+![]() x��6����5����ã�x��
x��6����5����ã�x��![]() �����������ֵ����ȥ����
�����������ֵ����ȥ����
�ʵ�P��![]() ����5����
����5����

�ڵ���H��y����ʱ��ͼ2�Ҳ�ͼ��ͬ���ɵã���P��![]() ��
��![]() ����
����
���ϣ���P������Ϊ����![]() ����5����
����5����![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() �����Խ���
�����Խ���![]() �е�
�е�![]() ��ֱ�߷ֱ�
��ֱ�߷ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
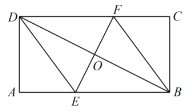
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2�����ı���![]() ������ʱ��������
������ʱ��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ���b��2a����a+2c��b��0����b��a��c����b2+2ac��3ab��������ȷ���۵ĸ����ǣ�������
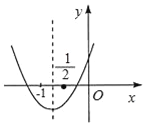
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����x�ĺ���y=k��x��1����y=![]() ��k��0����������ͬһ����ϵ�ڵ�ͼ������ǣ� ��
��k��0����������ͬһ����ϵ�ڵ�ͼ������ǣ� ��
A��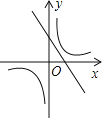 B��
B��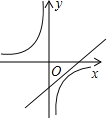 C��
C��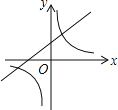 D��
D��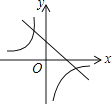
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A���߶�BG�ϣ�ABCD��DEFG���������Σ�����ֱ�Ϊ7��11������CDE��������� ��
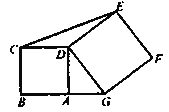
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����ι���![]() ��
��![]() ������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
�������������� | ����������� ��Ԫ�� | ||
A | B | ||
��һ�� | 20 | 50 | 4100 |
�ڶ��� | 30 | 40 | 3700 |
��1����![]() ��
��![]() ������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳�����![]() ��Ʒ��ÿ��50Ԫ���ۣ�
��Ʒ��ÿ��50Ԫ���ۣ�![]() ��Ʒ��ÿ��
��Ʒ��ÿ��![]() Ԫ���ۣ�Ϊ�����г������蹺��
Ԫ���ۣ�Ϊ�����г������蹺��![]() ��
��![]() ������Ʒ��
������Ʒ��![]() ������
������![]() ��Ʒ������������
��Ʒ������������![]() ��Ʒ������
��Ʒ������![]() ������������������Ľ�����������ȷ���������
������������������Ľ�����������ȷ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2��4x+c��ͼ������ԭ�㣬��x�ύ�ڵ�A����4��0����

��1������κ����Ľ���ʽ��
��2�����������ϴ��ڵ�P������S��AOP=8����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O������COB�Ƶ�O˳ʱ����ת������ת��Ϊ����0������90�������ǵ����߷ֱ���BC��AB���ڵ�M��N������DM��CN��MN�������ĸ����ۣ��١�CDM����COM����CN��DM������CNB�ա�DMC����AN2+CM2��MN2��������ȷ���۵ĸ����ǣ�������

A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+8��x���ཻ�ڵ�A����2��0���͵�B��4��0������y���ཻ�ڵ�C������Ϊ��P����D��0��4����OC�ϣ�����BC��BD��
��1���������ߵı���ʽ��ֱ��д����P�����ꣻ
��2����EΪ��һ��������������һ�㣬�����COE����BCD�������ȣ����E�����ꣻ
��3����Q�������߶Գ����ϣ������BCD�ס�CPQ�����Q�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com