
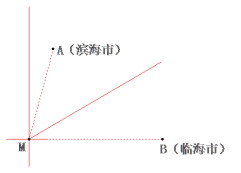
【题目】如图,在海面上生成了一股强台风,台风中心(记为点M)位于滨海市(记作点A)的南偏西15°,距离为![]() 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向![]() 千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
【答案】(1)滨海市不受影响,临海市受影响,理由见详解.
(2)![]() 小时.
小时.
【解析】
(1)过A作AH⊥MN于H,故AMH是等腰直角三角形,可求出AM,则可以判断滨海市是否会受到此次台风的侵袭.
同理,过B作BH1⊥MN于H1,求出BH1,可以判断临海市是否会受到此次台风的侵袭.
(2)求该城市受到台风侵袭的持续时间,以B为圆心60为半径作圆与MN交于T1、T2,则T1T2就是台风影响时经过的路径,求出后除以台风的速度就是时间.
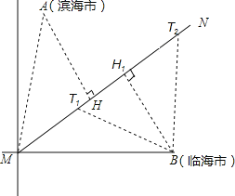
解:(1)设台风中心运行的路线为射线MN,于是![]() .
.
过A作AH⊥MN于H,故AMH是等腰直角三角形.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴滨海市不会受到台风的影响;
过B作BH1⊥MN于H1.
∵![]() ,
,![]() ,
,
∴![]() ,
,
因此临海市会受到台风的影响.
(2)以B为圆心60千米为半径作圆与MN交于T1、T2,则![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∴台风中心经过线段T1T2上所用的时间![]() 小时.
小时.
因此临海市受到台风侵袭的时间为![]() 小时.
小时.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
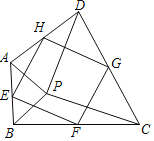
(1)如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(2)若改变(1)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有a2≥0成立,所以,当a=0时,a2有最小值0.
(应用):(1)代数式(x-1)2有最小值时,x=___1;
(2)代数式m2+3的最小值是____3;
(探究):求代数式n2+4n+9的最小值,小明是这样做的:
n2+4n+9
=n2+4n+4+5
=(n+2)2+5
∴当n=-2时,代数式n2+4n+9有最小值,最小值为5.
请你参照小明的方法,求代数式a2-6a-3的最小值,并求此时a的值.
(拓展):(3)代数式m2+n2-8m+2n+17=0,求m+n的值.
(4)若y=-4t2+12t+6,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等腰直角三角形,∠ACB=90°,点A在直线DE上,过C点作CF⊥DE于F,过B点作BG⊥DE于G.
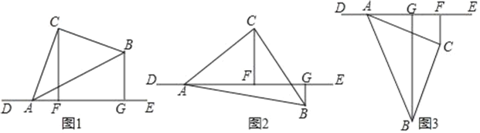
(1)发现问题:如图1,当B、C两点均在直线DE上方时,线段AG、BG和CF存在的数量关系是 .
(2)类比探究:当△ABC绕点A顺时针旋转至图2的位置时,线段AG、BG和CF之间的数量关系是否会发生变化?如果不变,请说明理由;如果变化,请写出你的猜想,并给予证明;
(3)拓展延伸:当△ABC绕点A顺时针旋转至图3的位置时,若CF=1,AG=2,请直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
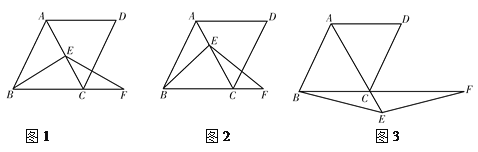
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC垂足为E.
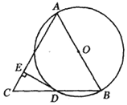
(1)求证:AB=AC;
(2)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com