
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
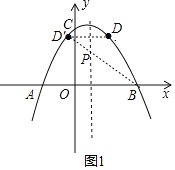
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
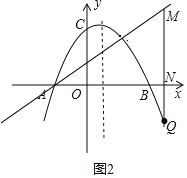
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)存在,理由见解析;(3)见解析.
x+3;(2)存在,理由见解析;(3)见解析.
【解析】
(1)点A、C的坐标分别为:(-2,0)、(0,3),将点A、C的坐标代入抛物线表达式,即可求解;
(2)作点D关于对称轴的对称轴D′(-1,2),连接BD′交抛物线对称轴与点P,则点P为所求,即可求解;
(3)QM=|-![]() m2+
m2+![]() m+3-
m+3-![]() m-1|=|-
m-1|=|-![]() m2+2|,3MN=3(
m2+2|,3MN=3(![]() m+1),QM=3MN,即|-
m+1),QM=3MN,即|-![]() m2+2|=3(
m2+2|=3(![]() m+1),即可求解.
m+1),即可求解.
解:(1)点A、C的坐标分别为:(﹣2,0)、(0,3),
将点A、C的坐标代入抛物线表达式得: ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)存在,理由:
作点D关于对称轴的对称轴D′(﹣1,2),连接BD′交抛物线对称轴与点P,则点P为所求,
将点B、D′的坐标代入一次函数表达式:y=kx+b并解得:
直线BD′的函数表达式为:y=﹣![]() x+
x+![]() ,
,
抛物线的对称轴为:x=![]() ,当x=
,当x=![]() 时,y=
时,y=![]() ,
,
故点P(![]() ,
,![]() );
);
(3)设点N(m,0),则点M、Q的坐标分别为:(m,![]() m+1)、(m,﹣
m+1)、(m,﹣![]() m2+
m2+![]() m+3),
m+3),
则QM=|﹣![]() m2+
m2+![]() m+3﹣
m+3﹣![]() m﹣1|=|﹣
m﹣1|=|﹣![]() m2+2|,
m2+2|,
3MN=3(![]() m+1),
m+1),
∵QM=3MN,即|﹣![]() m2+2|=3(
m2+2|=3(![]() m+1),
m+1),
解得:m=﹣2或﹣1或5,
故点Q(﹣2,3)或(﹣1,2)或(5,﹣7).


科目:初中数学 来源: 题型:
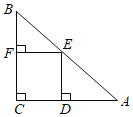
【题目】如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
A. B.
B. C.
C.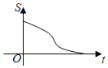 D.
D.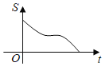
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
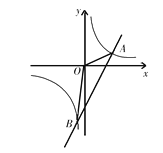
【题目】如图,直线y1=3x﹣5与反比例函数y2=![]() 的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
(1)求k和n的值;
(2)求△AOB的面积;
(3)直接写出y1> y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
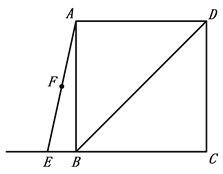
【题目】如图,在正方形ABCD中,连接BD,点E为CB边的延长线上一点,点F是线段AE的中点,过点F作AE的垂线交BD于点M,连接ME、MC.
(1)根据题意补全图形,猜想![]() 与
与![]() 的数量关系并证明;
的数量关系并证明;
(2)连接FB,判断FB 、FM之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
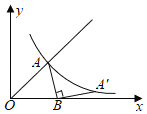
【题目】如图,函数y=x(x≥0)的图象与反比例函数y=![]() 的图象交于点A,若点A绕点B(
的图象交于点A,若点A绕点B(![]() ,0)顺时针旋转90°后,得到的点A'仍在y=
,0)顺时针旋转90°后,得到的点A'仍在y=![]() 的图象上,则点A的坐标为_____.
的图象上,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
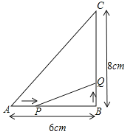
【题目】如图所示,在△ABC中,∠B=90°,点P从A点开始沿AB边向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动,若点P、Q分别从点A、B同时出发,问过多少秒后,△PBQ的面积分别为8cm2和10cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
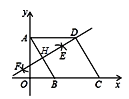
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
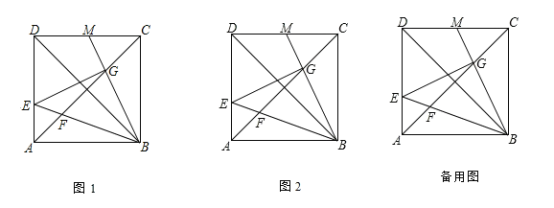
【题目】如图,在边长为6的正方形ABCD中,点E为AD边上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G、交CD于点M.
(1)如图1,联结BD,求证:![]() ,并写出
,并写出![]() 的值;
的值;
(2)联结EG,如图2,若设![]() ,求y关于
,求y关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当M为边DC的三等分点时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com