
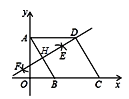
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
【答案】D
【解析】
连接DB,如图,利用基本作图得到EF垂直平分AB,则DA=DB,再根据菱形的性质得到AD∥BC,AD=AB,则可判断△ADB为等边三角形,所以∠DAB=∠ABO=60°,然后计算出AD=2,![]() ,从而四边形HBCD的周长.
,从而四边形HBCD的周长.
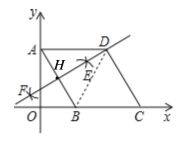
连接DB,如图,
由作法得EF垂直平分AB,
∴DA=DB,AH=BH,
∵四边形ABCD是菱形,
∴AD∥BC,AD=AB,
∴AD=AB=DB,
∴△ADB为等边三角形,
∴∠DAB=60°,
∴∠ABO=60°,
∵A(0,![]() ),
),
∴OA=![]() ,
,
∴OB=![]() OA=1,AB=2OB=2,
OA=1,AB=2OB=2,
∴AD=AB=2,
∴AH=1,
∴![]() ,
,
∴四边形HBCD的周长为:1+2+2+![]() =
=![]() ,
,
故选:D.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣3,0),C (4,0)两点,与y轴交于点B.
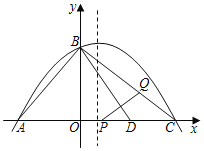
(1)求这条抛物线的顶点坐标;
(2)已知AD=AB(点D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个点Q以某一速度从点B沿线段BC移动,经过t(s)的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
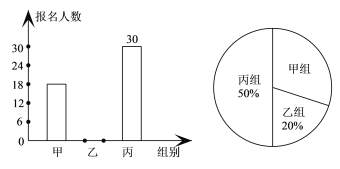
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
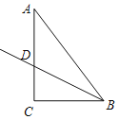
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若![]() ,AC=8,求DE的长.
,AC=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
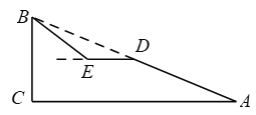
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com