
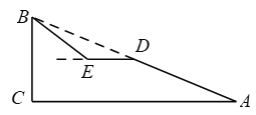
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
【答案】(1)25;(2)![]() 米
米
【解析】
(1)设BC=x,则AC=2.4x,在Rt△ABC中,利用勾股定理可求得x的值;
(2)如下图,延长DE交BC于F,根据点D是AB的中点,可推导得出点F是BC的中点,从而得出DF,BF的长,然后在Rt△BEF中,求得EF的长,最后得出DE的长.
(1)解:∵斜坡AB的长为65米,坡度i=1∶2.4,
∴可设BC=x,AC=2.4x,
在Rt△ABC中,BC2+AC2=AB2,即得x2+(2.4x)2=652,
解得x=25,
∴BC=25.
(2)解:延长DE交BC于F,
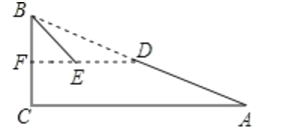
∵D是AB的中点,DE∥AC,∴BF=12.5米,
∴DF=12.5×2.4=30米,
∵tan37°=![]() ,
,
∴EF=![]() 米,
米,
∴DE=DF-EF=![]() 米.
米.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
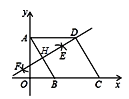
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
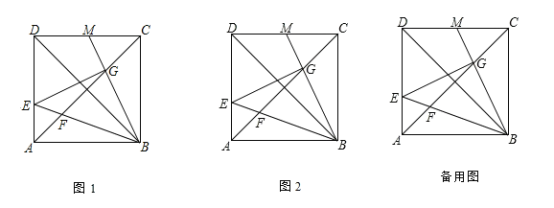
【题目】如图,在边长为6的正方形ABCD中,点E为AD边上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G、交CD于点M.
(1)如图1,联结BD,求证:![]() ,并写出
,并写出![]() 的值;
的值;
(2)联结EG,如图2,若设![]() ,求y关于
,求y关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当M为边DC的三等分点时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
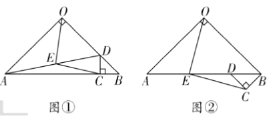
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是( )
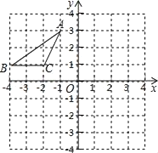
A.A1(4,4),C1(3,2)B.A1(3,3),C1(2,1)
C.A1(4,3),C1(2,3)D.A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在同一平面直角坐标系中有函数y1=ax2﹣2ax+b,y2=﹣ax+b,其中ab≠0.
(1)求证:函数y2的图象经过函数y1的图象的顶点;
(2)设函数y2的图象与x轴的交点为M,若点M关于y轴的对称点M'在函数y1图象上,求a,b满足的关系式;
(3)当﹣1<x<1时,比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
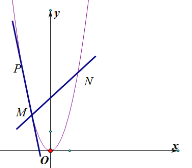
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
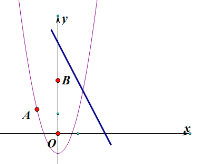
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com