
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������y����x2+bx+c��ֱ��y����x+1�ཻ�ڵ�A(0��1)�͵�B(3����2)����x���ڵ�C������Ϊ��F����D�Ǹ���������һ�㣮
��1���������ߵĺ�������ʽ��
��2����ͼ1������D��ֱ��AB�Ϸ����������ϣ�����DAB��������ʱ��D�����ꣻ
��3����ͼ2������D�ڶԳ��������������ϣ��ҵ�E��1��t��������CF��һ�㣬����C��B��DΪ���������������CAE����ʱ������������������t��ֵ��

���𰸡���1��y����x2+2x+1����2��![]() ����3��t��1��t��2��
����3��t��1��t��2��![]() ��
��![]()
��������
��1������A��0��1���͵�B��3��-2��������������y=-x2+bx+c�У��г������鼴�ɽ��
��2������D�� DM��y�ύAB�ڵ�M��D��a��-a2+2a+1������M��a��-a+1���������DM�������������ABD����������ö��κ��������ʵó����ֵ��D�����ꣻ
��3���������֪����ACE=��ACO=45�������BCD�б���һ���ڽ�Ϊ45���������������������CBD=45�����ó���BCD�ǵ���ֱ�������Σ���ˡ�ACEҲ�ǵ���ֱ�������Σ��ٌ���ACE���з�����i�ۣ�������CDB=45������Բ������ȷ��D1��λ�ã����D1�����꣬�ٶԡ�ACE���CD1B���Ʒ������ۣ�
�⣺��1������A��0��1���͵�B��3����2��������������y����x2+bx+c��
��![]() ��
��
���![]()
��y����x2+2x+1��
��2����ͼ1��ʾ������D�� DM��y�ύAB�ڵ�M��
��D��a����a2+2a+1������M��a����a+1��
����DM����a2+2a+1������a+1������a2+3a
��![]()
��![]()
![]() ��
��![]() �����ֵ��
�����ֵ��
��![]() ʱ��
ʱ��![]()
��ʱ![]()
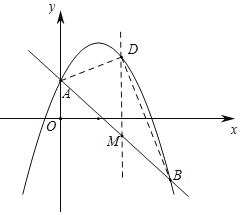
ͼ1
��3����OA��OC����ͼ2��CF��y�ᣬ
���ACE����ACO��45����
���BCD�б���һ���ڽ�Ϊ45�����������֪����BCD������Ϊ45����
������CBD��45������BD��x�ᣬ
���D���B�������ߵČ�����ֱ��x��1���ƣ���BD��ֱ�ߣ�1���ڵ�H����H��1����2��
B��3����2����D����1����2��
��ʱ��BCD�ǵ���ֱ�������Σ���ˡ�ACEҲ�ǵ���ֱ�������Σ�
��i������AEC��90��/span>ʱ���õ�AE��CE��1��
��E��1.1�����õ�t��1
��ii������CAE��90ʱ���õ���AC��AE��![]() ��
��
��CE��2����E��1.2�����õ�t��2
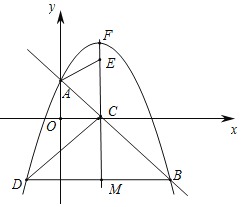
ͼ2
������CDB��45������ͼ3�����е����������һ�֣���ͬ��
�Ե�HΪԲ�ģ�HBΪ�뾶��Բ�����B��C��D����ԲH�ϣ�
��ԲH��Գ��������߽�����һ��D1��
���CD1B����CDB��45����ͬ�����Ե�Բ�ܽ���ȣ�����D1Ҳ��������
��![]()
��HD1��DH��2
���n1����1����ȥ����n2��3����ȥ����![]() ����ȥ����
����ȥ����![]()
��![]() ��
��
��![]() ��
��
![]()
��i������ACE�ס�CD1B��
��![]() ��
��
��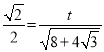 ��
��
���![]() ��
��![]() ����ȥ��
����ȥ��
��ii����ACE�ס�BD1C��![]() ��
��
��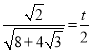 ��
��
���![]() ��
��![]() ����ȥ��
����ȥ��
������������������������t��ֵΪt��1��t��2��![]() ��
��![]()

ͼ3


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У��Խ���
�У��Խ���![]() �Ĵ�ֱƽ���߽�ֱ��
�Ĵ�ֱƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��Ϊ______��
��Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������̶ӹ�ͬ����һ����·���̣��ӵ���ʩ��3���£���ʱ�������Ҷӣ������ֹ�ͬ������2���£��ܹ���ȫ����ɣ���֪�ӵ������ȫ�����̱��Ҷӵ������ȫ�����̶���2���£���ӵ������ȫ��������![]() ���£������������з����д�����ǣ� ��
���£������������з����д�����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() �r
�r![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��ֱ��
��ֱ��![]() ��
��
(1)��![]() ʱ������ֱ��
ʱ������ֱ��![]() ��������
��������![]() ����ֱ��д��ֱ��
����ֱ��д��ֱ��![]() ��������
��������![]() �صõ��߶γ���
�صõ��߶γ���
(2)����![]() ȡֵ�ı仯���жϵ�
ȡֵ�ı仯���жϵ�![]() �Ƿ���ֱ��
�Ƿ���ֱ��![]() �ϲ�˵�����ɣ�
�ϲ�˵�����ɣ�
(3)��ֱ��![]() ��������
��������![]() �صõ��߶γ���С��3����Ϻ�����ͼ��ֱ��д��
�صõ��߶γ���С��3����Ϻ�����ͼ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ƽ���չ�����������й��ѽ�����ɫ���������ʱ����Ϊʵ��������һ�������ܶ�Ŀ����л�����ΰ���˵��й��Σ���Ҫ���˷ܶ���������ʱ��������Ʒ���γɺ�֪ʶ���۵Ļƽ�ʱ�ڣ�Ϊ�ˣ�������ƽ̨��Բ�����ѧ��Ʒ����ֺ�ѧϰ״�����е���ͳ�ƻ�������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣬���![]() Ʒ��ȫ���ɼ����죻
Ʒ��ȫ���ɼ����죻![]() ��ʦ����������ȡ��
��ʦ����������ȡ��![]() �Կ��������ѧϰ��
�Կ��������ѧϰ��![]() �������棬�����Ա���
�������棬�����Ա���
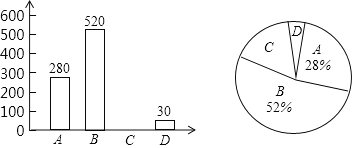
��1�����ε��鱻��ȡ����������Ϊ ��
��2�����Կ��������ѧϰ����ͬѧ�� �ˣ�����ȫ����ͳ��ͼ��
��3��������![]() ���������ε�Բ�Ľ�Ϊ �ȣ�
���������ε�Բ�Ľ�Ϊ �ȣ�
��4�������س���ij��ѧ����Уѧ��3330�ˣ�������У![]() ��ѧ��������
��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���С����д����ѧʵ�������IJ�������
�� Ŀ | �����������˵�����ĸ߶� | |
����Ŀ��ʾ��ͼ |
|
|
������� | CD=20m����=45������=52�� | |
�������ĸ߶�FE(�����ȷ��1��)���ο����ݣ�sin52���0.79�� cos52���0.62��tan52���1.28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
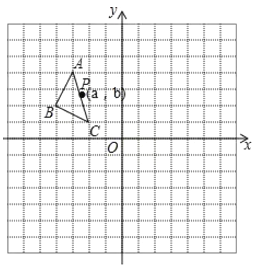
����Ŀ����ͼ��ʾ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ�
(1)����ABC����ƽ��5����λ������ƽ��1����λ��õ���Ӧ�ġ�A1B1C1��������A1B1C1��
(2)������A1B1C1����y��ԳƵġ�A2B2C2��
(3)P(a��b)�ǡ�ABC�ı�AC��һ�㣬��ֱ��д���������α任���ڡ�A2B2C2�ж�Ӧ�ĵ�P2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ���
��ֱ���![]() ���㣬�뷴��������
���㣬�뷴��������![]() ���ڵ�
���ڵ�![]() ��
��![]() ������Ϊ
������Ϊ![]() ���ڵ�
���ڵ�![]() ��
��

��1����![]() ������Ϊ ��
������Ϊ ��
��2������![]() Ϊ
Ϊ![]() ���е㣬��������
���е㣬��������![]() �Ľ���ʽ��
�Ľ���ʽ��
��3���ڣ�2�������£���![]() Ϊ��������������
��������������![]() ��
��![]() �ڵ�
�ڵ�![]() ֱ��д��
ֱ��д��![]() ���ܳ���
���ܳ���![]() ���ܳ��ıȣ�
���ܳ��ıȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͼ�������ʡ���չѧϰչʾ��
�����⣩��ͼ1����ƽ��ֱ������ϵ�У�������G1��![]() ��x���ཻ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C����a= ��b= ��
��x���ཻ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C����a= ��b= ��
����������ͼ1��������G1��BC����ƽ��BC���ȵľ���õ�������G2��G2��y�����IJ�����G1��y���Ҳ�IJ�����ɵ���ͼ���ΪG����ͼ�ڣ���ֱ��д��ͼ��G��Ӧ�ĺ�������ʽ��
��̽������ͼ2�У�����C��ֱ��lƽ����x�ᣬ��ͼ��G����D��E���㣮��ͼ��G��ֱ��l�Ϸ��IJ��ֶ�Ӧ�ĺ���y��x�����������ʱx��ȡֵ��Χ��
��Ӧ�ã�P��������G2�Գ�����һ�����㣬����PDE��ֱ��������ʱ��ֱ��д��P������꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com