
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+4ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈЉ3ЃЌ0ЃЉЃЌC ЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуBЃЎ
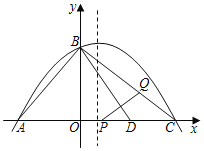
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉвбжЊADЃНABЃЈЕуDдкЯпЖЮACЩЯЃЉЃЌгавЛЖЏЕуPДгЕуAбиЯпЖЮACвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЛЭЌЪБСэвЛИіЕуQвдФГвЛЫйЖШДгЕуBбиЯпЖЮBCвЦЖЏЃЌОЙ§tЃЈsЃЉЕФвЦЖЏЃЌЯпЖЮPQБЛBDДЙжБЦНЗжЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуMЃЌЪЙMQ+MCЕФжЕзюаЁЃПШєДцдкЃЌЧыЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉетЬѕХзЮяЯпЕФЖЅЕузјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ2ЃЉtЃН
ЃЉЃЛЃЈ2ЃЉtЃН![]() ЃЛЃЈ3ЃЉДцдкЃЌMЃЈ
ЃЛЃЈ3ЃЉДцдкЃЌMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯпЭМЯёЩЯЕФШ§ЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтД№ЃЛ
ЃЈ2ЃЉИљОнAЁЂBЕФзјБъЃЌвзЧѓЕУAD=AB=5ЃЌдђCD=AC-AD=2ЃЌСЌНгDQЃЌгЩгкBDДЙжБЦНЗжPQЃЌФЧУДDP=DQЃЌИљОнЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪжЊЃКЁЯPDB=ЁЯQDB=ЁЯABDЃЌМДAB//DQЃЌДЫЪБЁїCDQЁзЁїCABЃЌРћгУЯрЫЦШ§НЧаЮЕУЕНЕФБШР§ЯпЖЮМДПЩЧѓЕУD QЁЂPDЕФГЄЃЌДгЖјЧѓЕУAPЕФжЕЃЌМДПЩЧѓЕУtЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЯШзїCЙигкЖдГЦжсЕФЖдГЦЕуЃЌМДЕуAЃЛСЌНгAQгыЖдГЦжсЕФНЛЕуОЭЪЧЫљЧѓЕФMЃЌЯШЧѓ2ЕФзјБъЃЌЧѓжБЯп42ЕФНтЮіЪНЃЌвђЮЊЖдГЦжсЪЧЃКx=![]() ЃЌМДMЕФКсзјБъОЭЪЧ
ЃЌМДMЕФКсзјБъОЭЪЧ![]() ЃЌДњШыAQЕФНтЮіЪНЧѓГіyЕФжЕЃЎ
ЃЌДњШыAQЕФНтЮіЪНЧѓГіyЕФжЕЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+4ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈЉ3ЃЌ0ЃЉЃЌC ЃЈ4ЃЌ0ЃЉСНЕуЃЌ
Ёр![]() ЃЎ
ЃЎ
НтетИіЗНГЬЃЌЕУ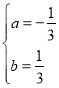
ЁрИУХзЮяЯпНтЮіЪНЪЧyЃНЉ![]() x2+
x2+![]() x+4ЃЎ
x+4ЃЎ
ЁпyЃНЉ![]() x2+
x2+![]() x+4ЃНyЃНЉ
x+4ЃНyЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЎ
ЃЎ
ЁретЬѕХзЮяЯпЕФЖЅЕузјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЁпAЃЈЉ3ЃЌ0ЃЉЃЌC ЃЈ4ЃЌ0ЃЉЃЌ
ЁрOAЃН3ЃЌOBЃНOCЃН4ЃЌ
дђABЃН5ЃЌACЃН7ЃЌCDЃН2ЃЛ
ШчЭМ1ЃЌСЌНгDQЃЌгЩгкBDДЙжБЦНЗжPQЃЌдђDPЃНDQЃЌЕУЃК
ЁЯPDBЃНЁЯQDBЃЌ
ЖјADЃНABЃЌЕУЃКЁЯABDЃНЁЯADBЃЌ
ЙЪЁЯQDBЃНЁЯABDЃЌ
ЕУQDЁЮABЃЛ
ЁрЁїCDQЁзЁїCABЃЌдђгаЃК![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрPDЃНDQЃН![]() ЃЌAPЃНADЉPDЃН5Љ
ЃЌAPЃНADЉPDЃН5Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЙЪtЃН![]() ЃЛ
ЃЛ
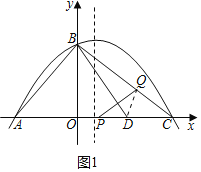
ЃЈ3ЃЉДцдкЃЌ
ШчЭМ2ЃЌСЌНгAQНЛЖдГЦжсгкMЃЌДЫЪБMQ+MCЮЊзюаЁЃЌ
Й§QзїQNЁЭxжсгкNЃЌ
ЁпDQЁЮABЃЌ
ЁрЁЯQDNЃНЁЯBACЃЌ
sinЁЯQDNЃНsinЁЯBACЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрQNЃН![]() ЃЌ
ЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊЃКyЃНkx+bЃЌ
АбBЃЈ0ЃЌ4ЃЉКЭCЃЈ4ЃЌ0ЃЉДњШыЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊЃКyЃНЉx+4ЃЌ
ЕБyЃН![]() ЪБЃЌ
ЪБЃЌ![]() ЃНЉx+4ЃЌ
ЃНЉx+4ЃЌ
xЃН![]() ЃЌ
ЃЌ
ЁрQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЭЌРэПЩЕУЃКAQЕФНтЮіЪНЮЊЃКyЃН![]() x+
x+![]() ЃЌ
ЃЌ
ЕБxЃН![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЁС
ЁС![]()
![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃНBCЃН2ЃЌPЮЊACЕФжаЕуЃЌQЮЊABЩЯЕФвЛИіЖЏЕуЃЌСЌНгPQЃЌCQЃЌдђPQ+CQЕФзюаЁжЕЮЊЃЈЁЁЁЁЃЉ
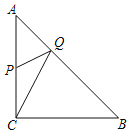
A.2B.3C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧШ§НЧаЮABCжаЃЌЁЯCЃН90ЁуЃЌACЃНBCЃЌEЪЧABЕФжаЕуЃЌЙ§ЕуEзїACКЭBCЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуDКЭЕуFЃЌЫФБпаЮCDEFбизХCAЗНЯђдШЫйдЫЖЏЃЌЕуCгыЕуAжиКЯЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtЃЌдЫЖЏЙ§ГЬжаЫФБпаЮCDEFгыЁїABCЕФжиЕўВПЗжУцЛ§ЮЊSЃЎдђSЙигкtЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈЁЁЁЁЃЉ
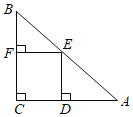
A. B.
B.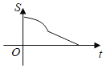 C.
C.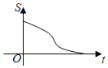 D.
D.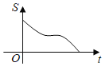
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCЪЧЛЁBEжаЕуЃЌAEЁЭCDгкЕуDЃЌбгГЄDCЃЌABНЛгкЕуFЃЌвбжЊADЃН4ЃЌFCЃН![]() FBЃЎ
FBЃЎ
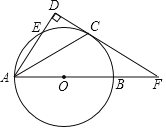
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉЧѓЯпЖЮFCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
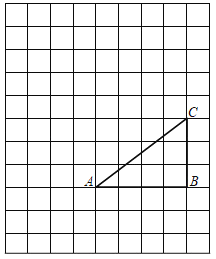
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCЗХдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌЕуAЁЂBЁЂCОљдкИёЕуЩЯЃЎ
ЃЈ1ЃЉБпACЕФГЄЕШгк_____ЃЎ
ЃЈ2ЃЉвдЕуCЮЊа§зЊжааФЃЌАбЁїABCЫГЪБеыа§зЊЃЌЕУЕНЁїA'B'C'ЃЌЪЙЕуBЕФЖдгІЕуB'ЧЁКУТфдкБпACЩЯЃЌЧыдкШчЭМЫљЪОЕФЭјИёжаЃЌгУЮоПЬЖШЕФжБГпЃЌзїГіа§зЊКѓЕФЭМаЮЃЌВЂМђвЊЫЕУїзїЭМЕФЗНЗЈЃЈВЛвЊЧѓжЄУїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖСЪщдТЛюЖЏжаЃЌбЇаЃзМБИЙКТђвЛХњПЮЭтЖСЮяЃЎЮЊЪЙПЮЭтЖСЮяТњзуЭЌбЇУЧЕФашЧѓЃЌбЇаЃОЭЁАЮвзюЯВАЎЕФПЮЭтЖСЮяЁБДгЮФбЇЁЂвеЪѕЁЂПЦЦеКЭЦфЫћЫФИіРрБ№НјааСЫГщбљЕїВщЃЈУПЮЛЭЌбЇжЛбЁвЛРрЃЉЃЌШчЭМЪЧИљ
ОнЕїВщНсЙћЛцжЦЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыФуИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщжаЃЌвЛЙВЕїВщСЫЁЁ ЁЁУћЭЌбЇЃЛ
ЃЈ2ЃЉЬѕаЮЭГМЦЭМжаЃЌm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЛ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЃЌвеЪѕРрЖСЮяЫљдкЩШаЮЕФдВаФНЧЪЧЁЁ ЁЁЖШЃЛ
ЃЈ4ЃЉбЇаЃМЦЛЎЙКТђПЮЭтЖСЮя6000ВсЃЌЧыИљОнбљБОЪ§ОнЃЌЙРМЦбЇаЃЙКТђЦфЫћРрЖСЮяЖрЩйВсБШНЯКЯРэЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаМЦЛЎЙКНјМзЁЂввСНжжЩЬЦЗЃЌСНжжЩЬЦЗЕФНјМлЁЂЪлМлШчЯТБэЃК
ЩЬЦЗ | Мз | вв |
НјМлЃЈдЊ/МўЃЉ |
|
|
ЪлМлЃЈдЊ/МўЃЉ | 200 | 100 |
ШєгУ360дЊЙКНјМзжжЩЬЦЗЕФМўЪ§гыгУ180дЊЙКНјввжжЩЬЦЗЕФМўЪ§ЯрЭЌЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНжжЩЬЦЗЕФНјМлЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєГЌЪаЯњЪлМзЁЂввСНжжЩЬЦЗЙВ50МўЃЌЦфжаЯњЪлМзжжЩЬЦЗЮЊ![]() МўЃЈ
МўЃЈ![]() ЃЉЃЌЩшЯњЪлЭъ50МўМзЁЂввСНжжЩЬЦЗЕФзмРћШѓЮЊ
ЃЉЃЌЩшЯњЪлЭъ50МўМзЁЂввСНжжЩЬЦЗЕФзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
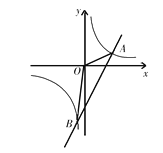
ЁОЬтФПЁПШчЭМЃЌжБЯпy1=3xЉ5гыЗДБШР§КЏЪ§y2=![]() ЕФЭМЯѓЯрНЛAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ6ЃЉСНЕуЃЌСЌНгOAЃЌOBЃЎ
ЕФЭМЯѓЯрНЛAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ6ЃЉСНЕуЃЌСЌНгOAЃЌOBЃЎ
ЃЈ1ЃЉЧѓkКЭnЕФжЕЃЛ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіy1ЃО y2ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
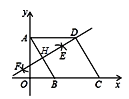
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮABCDЪЧСтаЮЃЌЕуAЕФзјБъЮЊ(0ЃЌ![]() )ЃЌЗжБ№вдAЃЌBЮЊдВаФЃЌДѓгк
)ЃЌЗжБ№вдAЃЌBЮЊдВаФЃЌДѓгк![]() ABЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкEЃЌFСНЕуЃЌжБЯпEFЧЁКУОЙ§ЕуDЃЌНЛABгкЕуHЃЌдђЫФБпаЮHBCDЕФжмГЄЮЊ(ЁЁЁЁ)
ABЕФГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкEЃЌFСНЕуЃЌжБЯпEFЧЁКУОЙ§ЕуDЃЌНЛABгкЕуHЃЌдђЫФБпаЮHBCDЕФжмГЄЮЊ(ЁЁЁЁ)
A.![]() B.6C.
B.6C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com