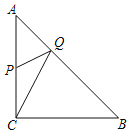
【题目】如图，在直角△ABC中，∠C＝90°，AC＝BC＝2，P为AC的中点，Q为AB上的一个动点，连接PQ，CQ，则PQ+CQ的最小值为（ ）
A.2B.3C.
D.
【答案】D
【解析】
过点P作点P关于AB的对称点P'，连接P'C，交AB点Q'，连接AP'．则AP＝AP'，PQ'＝P'Q'，当P'、Q'、C在同一直线上时，PQ＋CQ的最小值为CP'．由勾股定理得，CP'＝
=
=
，即PQ＋CQ的最小值为 .
如图，过点P作点P关于AB的对称点P'，连接P'C，交AB点Q'，连接AP'，
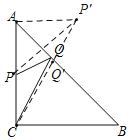
则AP＝AP'，PQ'＝P'Q'，
PQ+CQ＝P'Q+CQ
P'Q'+CQ'＝CP'，
即当P'、Q'、C在同一直线上时，PQ+CQ的最小值为CP'．
∵直角△ABC中，∠C＝90°，
∴∠CAB＝45°，∠P'AC＝45°，
∴∠CAP'＝90°，
∵AC＝BC＝2，P为AC的中点，
∴AP'＝AP＝1，
∴CP'＝==，
即PQ＋CQ的最小值为.
故选：D．
小学学习好帮手系列答案
小学同步三练核心密卷系列答案科目：初中数学 来源： 题型：
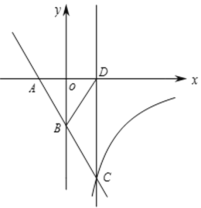
【题目】已知直线：y1＝
与x轴、y轴相交于A、B两点，与双曲线
(k＜0，x＞0)相交于第四象限的点C，过点C作直线l⊥x轴，垂足为D，若△ABD的面积为
，且B是AC的中点．
(1)求k的值；
(2)直接写出
的解集；
(3)若P为直线l的一动点，点P的纵坐标为m，∠APB≥30°，求m的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
图象的一部分如图所示，给出以下结论：
；
当
时，函数有最大值；
方程
的解是
，
；
，其中结论错误的个数是
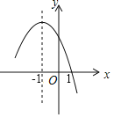
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
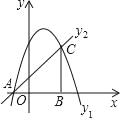
【题目】如图，抛物线y1＝a（x﹣1）2+4与x轴交于A（﹣1，0）．
（1）求该抛物线所表示的二次函数的表达式；
（2）一次函数y2＝x+1的图象与抛物线相交于A，C两点，过点C作CB垂直于x轴于点B，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们把图1称为一个基本图形，显然这个基本图形中有6个矩形，将此基本图形不断复制并向上平移、叠加，这样得到图2，图3…（如图所示）
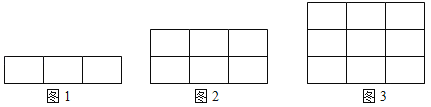
（1）观察图形，完成如表：
图形名称 | 矩形个数 |
图1 | 6 |
图2 | 18 |
图3 | 36 |
图4 | 60 |
图5 |
|
（2）根据以上规律猜想，图形n中共有多少个矩形（用含n的代数式表示）？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A在反比例函数y=
（x＞0）的图像上，点B在反比例函数y=
（x＞0）的图像上，AB∥x轴，BC⊥x轴，垂足为C，连接AC，若△ABC的面积是6，则k的值为（ ）
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分8分，每小题4分）
袋子中装有2个红球，1个黄球，它们除颜色外其余都相同。小明和小英做摸球游戏，约定一次游戏规则是：小英先从袋中任意摸出1个球记下颜色后放回，小明再从袋中摸出1个球记下颜色后放回，如果两人摸到的球的颜色相同，小英赢，否则小明赢．
（1）请用树状图或列表格法表示一次游戏中所有可能出现的结果；
（2）这个游戏规则对双方公平吗？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2+bx+4（a≠0）与x轴交于A（﹣3，0），C （4，0）两点，与y轴交于点B．
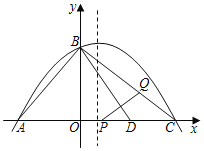
（1）求这条抛物线的顶点坐标；
（2）已知AD＝AB（点D在线段AC上），有一动点P从点A沿线段AC以每秒1个单位长度的速度移动；同时另一个点Q以某一速度从点B沿线段BC移动，经过t（s）的移动，线段PQ被BD垂直平分，求t的值；
（3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ+MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
