
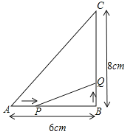
【题目】如图所示,在△ABC中,∠B=90°,点P从A点开始沿AB边向B点以1cm/s的速度移动,点Q从B点开始沿BC边向C点以2cm/s的速度移动,若点P、Q分别从点A、B同时出发,问过多少秒后,△PBQ的面积分别为8cm2和10cm2?
科目:初中数学 来源: 题型:
【题目】如图,四边形纸片ABCD中,AD∥BC,∠B=90°,BC=CD=6, ∠C=60°.点E是边AD上一点,连接BE,将△ABE沿BE翻折得到△HBE .
(1)当点B、D、H三点在一直线上时,求线段AE的长;
(2)当点A的对称点H正好落在DC上时,有动点P从点H出发沿线段HB向点B运动,同时动点Q从点B出发沿线段BA向点A运动,速度均为每秒1个单位长度,连接PQ交折痕BE于点M.设运动时间为t秒.
① 探究:当时间t为何值时,△PBM为等腰三角形;
② 连接AM,请直接写出BM+2AM的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=2∠C,以点A为圆心,AB长为半径作弧,交BC于点D,交AC于点G;再分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
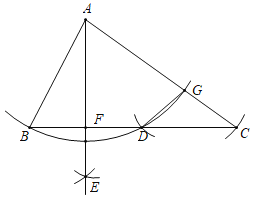
A.54°B.60°C.66°D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是AB上一点,以点D为圆心,AC为半径画弧交BA的延长线于点E,连接CD,作EF∥CD,交∠EAC的平分线于点F,连接CF.
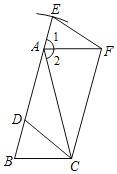
(1)求证:△BCD≌△AFE;
(2)若AC=6,∠BAC=30°,求四边形CDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
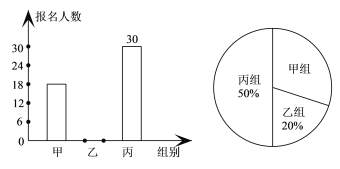
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
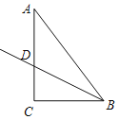
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com