
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
【答案】(1)通过证明OM⊥AE即可证明AE与⊙O相切。
(2)半径为![]()
【解析】试题分析:(1)连接OM.根据OB=OM,得∠OMB=∠OBM,结合BM平分∠ABC交AE于点M,得∠OBM=∠EBM,则OM∥BE;根据等腰三角形三线合一的性质,得AE⊥BC,则OM⊥AE,从而证明结论;(2)设圆的半径是r.根据等腰三角形三线合一的性质,得BE=CE=2,再根据解直角三角形的知识求得AB=6,则OA=6-r,从而根据平行线分线段成比例定理求解;
试题解析:
(1) 连接OM,则OM=OB,如图所示:
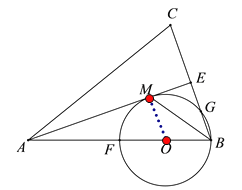
∴∠OBM=∠OMB
∵BM平分∠ABC
∴∠OBM=∠EBM
∴∠OMB=∠EBM
∴OM∥BE
∴∠AMO=∠AEB
而在⊿ABC中,AB=AC,AE是角平分线
∴AE⊥BC
∴∠AMO=∠AEB=90°
∴AE与⊙O相切.
(2) 在⊿ABC中,AB=AC,AE是角平分线
∴BE=![]() BC=2,∠ABC=∠ACB
BC=2,∠ABC=∠ACB
∴在Rt⊿ABC中cos∠ABC=cos∠ACB=![]() =
=![]()
∴AB=6
设⊙O的半径为r,则AO=6-r
∵OM∥BC
∴△AOM∽△ABE
∴![]() =
=![]()
即 ![]() =
=![]()
∴r=![]()


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】2017年,我国网络购物市场交易规模达61000亿元,较2016年增长29.6%.61000亿用科学记数法表示为( )
A. 6.1×1012B. 6.1×1011C. 6.1×108D. 6.1×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在给定的条件中,能作出平行四边形的是( )
A. 以60cm为对角线,20cm、34cm为两条邻边
B. 以20cm、36cm为对角线,22cm为一条边
C. 以6cm为一条对角线,3cm、10cm为两条邻边
D. 以6cm、10cm为对角线,8cm为一条边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( ) 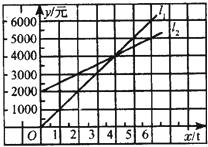
A.小于3t
B.大于3t
C.小于4t
D.大于4t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团25人准备同时租用这三种客房共9间,如果每个房间都住满,则租房方案共有( )
A.4种
B.3种
C.2种
D.1种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(-3,0),B(0, ![]() ),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
(1)求点C、点D的坐标并用尺规作图确定两点位置(保留作图痕迹)
(2)若半径为1的⊙P从点A出发,沿A—D—B—C以每秒4个单位长的速度匀速移动,同时⊙P的半径以每秒0.5个单位长的速度增加,运动到点C时运动停止,当运动时间为t秒时
①t为何值时,⊙P与y轴相切?
②在整个运动过程中⊙P与y轴有公共点的时间共有几秒?简述过程.
(3)若线段AB绕点O顺时针旋转90°,线段AB扫过的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
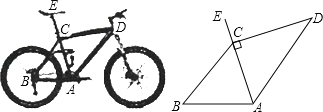
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
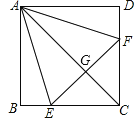
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com