
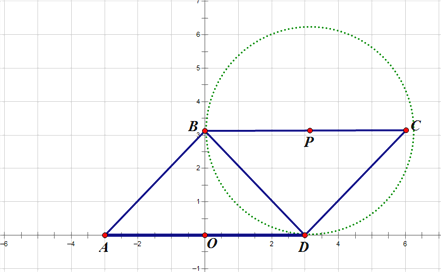
【题目】如图,在平面直角坐标系中,已知A(-3,0),B(0, ![]() ),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
),点D与点A关于y轴对称,C在第一象限内且四边形ABCD是平行四边形.
(1)求点C、点D的坐标并用尺规作图确定两点位置(保留作图痕迹)
(2)若半径为1的⊙P从点A出发,沿A—D—B—C以每秒4个单位长的速度匀速移动,同时⊙P的半径以每秒0.5个单位长的速度增加,运动到点C时运动停止,当运动时间为t秒时
①t为何值时,⊙P与y轴相切?
②在整个运动过程中⊙P与y轴有公共点的时间共有几秒?简述过程.
(3)若线段AB绕点O顺时针旋转90°,线段AB扫过的面积是多少?

【答案】(1)C(6,3![]() ), D(3,0) ;(2)①
), D(3,0) ;(2)①![]() ,
, ![]() ,
,![]() ,
, ![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由题可知:AD=AB=6,∠DAB=60°,再根据条件就可求出OB及BC的长,从而得到点C和点D的坐标.以点A为圆心,AB为半径画弧,与x轴交点即为点D;以点D为圆心,AB为半径画弧,以点B为圆心,AD为半径画弧,两弧的交点即为点C.
(2)①分点P在AO、OD、BD、BC上四种情况讨论,然后在直角三角形中运用特殊角的三角函数值建立方程,就可解决问题;
②只需求出三个临界位置(点P分别在AO、OD、BD、BC上,且⊙P与y轴相切)对应的t的值,就可解决问题.
(3)过点O作OH⊥AB,垂足为H,过点O作OH′⊥A′B′,垂足为H′,采用割补法将S阴影转化为S弓形AR+S△OHB+S扇形OBB′-S扇形OHH′-S△OH′B′就可解决问题.
试题解析:
(1)由题可知:AD=AB=6,∠DAB=60°.
∵∠AOB=90°,∴AO=3,OB=3![]()
∴OD=AD-OA=3.
∵四边形ABCD是平行四边形,
∴BC=AD=6.
∴点C的坐标为(6,3![]() ),点D的坐标为(3,0).
),点D的坐标为(3,0).
作法:①以点A为圆心,AB为半径画弧,与x轴交点即为点D;
②以点D为圆心,AB为半径画弧;以点B为圆心,AD为半径画弧,两弧的交点即为点C.
如图1所示.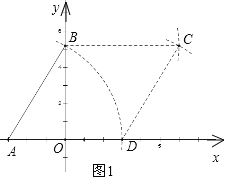
(2)①当点P在AO上时,如图所示:
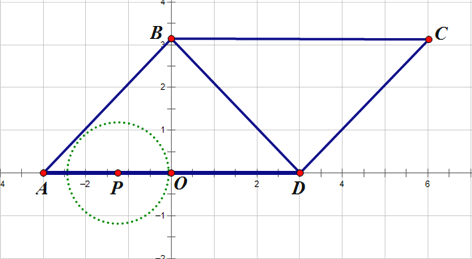
设时间为t,则r=1+0.5t,此时⊙P与y轴相切,
则AP=4t
∵AP+OP=AO
∴4t+1+0.5t=3,
∴t=![]() ;
;
当点P在OD上时,如图所示:
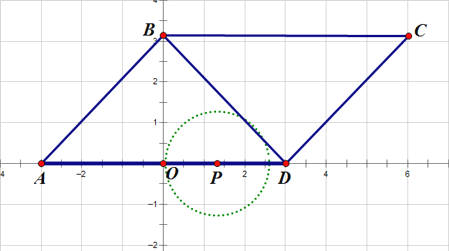
设时间为t,则r=1+0.5t,此时⊙P与y轴相切,
OP=4t-3,
∴4t-3=1+0.5t,
∴t=![]() ,
,
当点P在BD上时,作PE![]() OB,如图所示:
OB,如图所示:
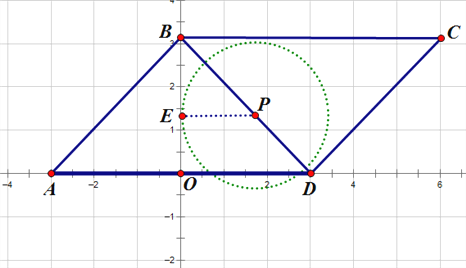
设时间为t,则r=1+0.5t,此时⊙P与y轴相切,
由PD=4t-6,
∵BD=![]() ,BP=BD-DP,
,BP=BD-DP,
∴BP=6-(4t-6)=12-4t,
∵cos∠ODB=![]() , ∠ODB=∠EPB
, ∠ODB=∠EPB
∴cos∠EPB=![]()
∴t=2;
当点P在BC上时,如图所示:
设时间为t,则r=1+0.5t,此时⊙P与y轴相切,
PB=4t-12
∴4t-12=1+0.5t
∴t=![]() ;
;
∴当运动时间为![]() 、
、![]() 、
、![]() 、
、![]() 时,⊙P与y轴相切;
时,⊙P与y轴相切;
②当圆P在AO上与y轴相切至圆P在OD上与y轴相切时,圆与y轴有交点,则时间为: ![]() ,当圆P在BD上与y轴相切至圆P在BC上与y轴相切时,圆与y轴有交点,则时间为:
,当圆P在BD上与y轴相切至圆P在BC上与y轴相切时,圆与y轴有交点,则时间为: ![]() ,所以总时间为
,所以总时间为![]() ;
;
(3)若线段AB绕点O顺时针旋转90°,线段AB扫过的图形如图8所示,
过点O作OH⊥AB,垂足为H,过点O作OH′⊥A′B′,垂足为H′,如图所示,
则有OH=OAsin∠HAO=3×![]() ,
,
同理可得:OH′=![]() ,
,
∵S弓形AR=S扇形OAR-S正△OAR=![]() ,
,
S扇形OBB′= ,
,
S扇形OHH′=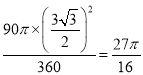
S△OHB=S△OH′B′
∴S阴影=S弓形AR+S△OHB+S扇形OBB′-S扇形OHH′-S△OH′B′
=S弓形AR+S扇形OBB′-S扇形OHH′
=![]()
=![]()
∴线段AB扫过的面积是![]() 。
。


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2 . S1与t之间的函数关系如图所示,请你解答下列问题: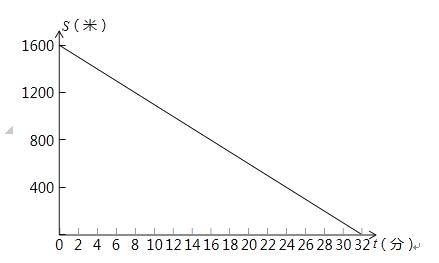
(1)李老师步行的速度为。
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
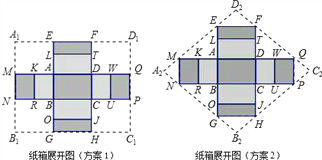
【题目】葡萄在销售时,要求“葡萄”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面面积的2倍),如图
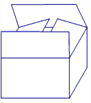
(1)实际运用:如果要求纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比, 取黄金比为0.6),体积为0.3立方米.
①按方案1(如图)做一个纸箱,需要矩形硬纸板A1B1C1D1的面积是多少平方米?
②小明认为,如果从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2 做一个纸箱比方案1更优,你认为呢?请说明理由.
(2)拓展思维:水果商打算在产地购进一批“葡萄”,但他感觉(1)中的纸箱体积太大,搬运吃力,要求将纸箱的底面周长、底面面积和高都设计为原来的一半,你认为水果商的要求能办到吗?请利用函数图象验证.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com