
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
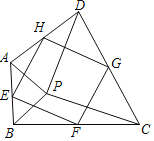
��1����ͼ����P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��2�����ı䣨1���е�������ʹ��APB����CPD��90���������������䣬ֱ��д���е��ı���EFGH����״������֤������
���𰸡���1���ı���EFGH�����Σ����ɼ���������2���ı���EFGH�������Σ����ɼ�����
��������
��1������AC��BD����PA��PB��PC��PD����APB����CPD��֤��APC�ա�BPD��SAS����
�ʿɵõ�AC��BD�������������ε���λ�߿ɵ�EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
��2����AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
���á�APC�ա�BPD�����ԡ�ACP����BDP���ٸ��ݡ�CPD��90���ʡ�PDC+��PCD��90��
�á�ODC+��OCD��90��������COD��90������AC��BD����������λ�ߵ����ʡ�EHG����ENO����BOC����DOC��90�������ɵõ��ı���EFGH�������Σ�
��1���ı���EFGH�����Σ�
��ͼ������AC��BD��

�ߡ�APB����CPD��
���APB+��APD����CPD+��APD������APC����BPD��
�ڡ�APC�͡�BPD�У�
 ��
��
���APC�ա�BPD��SAS����
��AC��BD��
�ߵ�E��F��G�ֱ�ΪAB��BC��CD���е㣬
��EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC��
AC��
��EF��FG��GH��EH��
���ı���EFGH�����Σ�
��2���ı���EFGH�������Σ�
��AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD��
���ACP����BDP��
�ߡ�CPD��90��
���PDC+��PCD��90��
���ODC+��OCD��90��
���COD��90��
��AC��BD
��EH��BD��AC��HG��
���EHG����ENO����BOC����DOC��90����
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
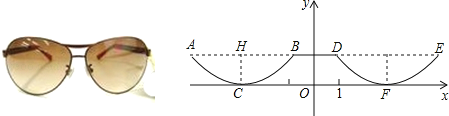
����Ŀ����ͼ��һ���۾���Ƭ�°벿��������Ӧ�����������߹���y��Գƣ�AB��x�ᣬAB=4cm����͵�C��x���ϣ���CH=1cm��BD=2cm������������DFE���������ߵĺ�������ʽΪ�� ��
A��y=![]() ��x+3��2
��x+3��2
B��y=![]() ��x+3��2
��x+3��2
C��y=![]() ��x��3��2
��x��3��2
D��y=![]() ��x��3��2
��x��3��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����У���������б�ʱ���мס����������̶�Ͷ�꣬�����㣺�ӵ�������������Ҫ60�죬����ɼ�����20�죬ʣ�µĹ����ɼס��Һ���24����ɣ�
��1���Ҷӵ�������������Ҫ�����죿
��2����ʩ��һ�죬��Ҫ֧�����̿�3.5��Ԫ���Ҷ�ʩ��һ����Ҫ֧�����̿�2��Ԫ������涨��70�����������������ɼס������ӵ������ʡǮ�������ɼ��Һ�����ɸù���ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���![]() ���������������ʵ����
���������������ʵ����![]() ��
��![]() ����ô
����ô![]() ��
��![]() ��˵������������������
��˵������������������![]() ��.���緽��
��.���緽��![]() �У�
�У�![]() �����Ը÷������������ȵ�ʵ����.�跽�̵�����Ϊ
�����Ը÷������������ȵ�ʵ����.�跽�̵�����Ϊ![]() ��
��![]() ����ô
����ô![]() ��
��![]() ������������Ķ����Ͻ�����и��⣺
������������Ķ����Ͻ�����и��⣺
��1����֪����![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
��2����֪![]() ��
��![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ�������Ƿ����ʵ��
������ʵ�������Ƿ����ʵ��![]() ��ʹ
��ʹ![]() �����������ڣ����
�����������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��6��BC��8����E��BC����һ�㣬����AE���ѡ�B��AE�۵���ʹ��B���ڵ�B�䴦������CEB��Ϊֱ��������ʱ��BE�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϰ���У���ʦ��������x�ĺ���y=2kx2-��4k+1��x-k+1��k��ʵ��������ʦ�������˼��������̽�����ֵ���ú����йصĽ��ۣ����ʣ�д���ڰ��ϣ�ѧ��˼���ڰ��ϳ�����һЩ���ۣ���ʦ��Ϊ�һԱ���ֲ���һЩ���ۣ�������ѡ������������
�����ں�������ͼ����1��0���㣻
�����ں������ú����ĺ���ֵyʼ����x���������С��
������ͼ���п��ܾ����������ޣ�
�������������ֵ�������ֵ��Ϊ����������������Сֵ������Сֵ��Ϊ������
������ȷ�Ľ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ1��������ABCD�Ƶ�A��ʱ����ת45���õ�������AB1C1D1����B1C1��CD���ڵ�O�����ı���AB1OD���������____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
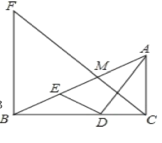
����Ŀ����ͼ,Rt��ABC��,AC��BC,ADƽ�֡�BAC��BC�ڵ�D,DE��AD��AB�ڵ�E,MΪAE���е�,BF��BC��CM���ӳ����ڵ�F,BD=4,CD=3.���н��ۣ��١�AED=��ADC;��![]() ;��AC
;��AC![]() BE=12;��3BF=4AC;������ȷ���۵ĸ�����( )
BE=12;��3BF=4AC;������ȷ���۵ĸ�����( )
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
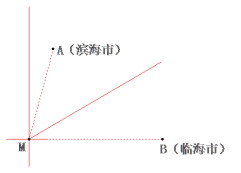
����Ŀ����ͼ���ں�����������һ��ǿ̨�磬̨�����ģ���Ϊ��M��λ�ڱ����У�������A������ƫ��15��������Ϊ![]() ǧ�ף���λ���ٺ��У�������B����������
ǧ�ף���λ���ٺ��У�������B����������![]() ǧ�״���̨����������72ǧ��/ʱ���ٶ��ر�ƫ��60���ķ����ƶ�������̨�����ƶ������еķ������ֲ��䣩������̨������60ǧ��Բ�������ھ����ܵ��˴�ǿ̨�����Ϯ��
ǧ�״���̨����������72ǧ��/ʱ���ٶ��ر�ƫ��60���ķ����ƶ�������̨�����ƶ������еķ������ֲ��䣩������̨������60ǧ��Բ�������ھ����ܵ��˴�ǿ̨�����Ϯ��
��1�������С��ٺ����Ƿ���ܵ��˴�̨�����Ϯ����˵�����ɣ�
��2�����ܵ��˴�̨����Ϯ���ó����ܵ�̨����Ϯ�ij���ʱ���ж���Сʱ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com