
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是(____)

【答案】![]() -1
-1
【解析】
连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.
解:连接AC1,
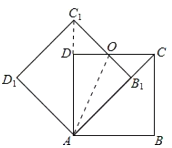
∵四边形AB1C1D1是正方形,
∴∠C1AB1=![]() ×90°=45°=∠AC1B1,
×90°=45°=∠AC1B1,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,
∴∠B1AB=45°,
∴∠DAB1=90°45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1D1A中,由勾股定理得:AC1=![]() ,
,
则DC1=![]() 1,
1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD=![]() 1,
1,
∴△C1DO的面积=![]() ODDC1=
ODDC1=![]() ,
,
∴四边形AB1OD的面积是=![]() =
=![]() 1.
1.
故答案为:![]() 1.
1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的方程y=- ![]() (x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
(x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
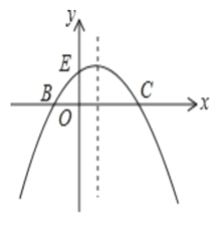
(1)求该抛物线的解析式
(2)在(1)的条件下,求△BCE的面积
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使EH+BH的值最小。求出点H的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
(1).求证:![]() ;
;
(2).点![]() 从点
从点![]() 出发,沿着线段
出发,沿着线段![]() 向点
向点![]() 运动(不与点
运动(不与点![]() 重合),同时点
重合),同时点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的延长线运动,点
的延长线运动,点![]() 与
与![]() 的运动速度相同,当动点
的运动速度相同,当动点![]() 停止运动时,另一动点
停止运动时,另一动点![]() 也随之停止运动.如图2,
也随之停止运动.如图2,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,请猜想
,请猜想![]() ,
,![]() 与
与![]() 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3).在(2)的条件下,当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
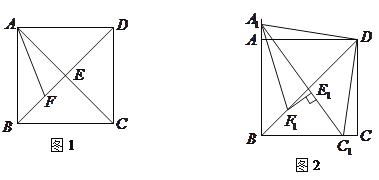
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
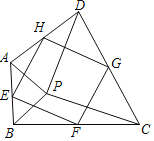
(1)如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(2)若改变(1)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,则下列各式正确的是( )①AD2=BDDC;②CD2=CFCA;③DE2=AEAB;④AEAB=AFAC.
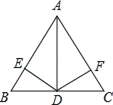
A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有a2≥0成立,所以,当a=0时,a2有最小值0.
(应用):(1)代数式(x-1)2有最小值时,x=___1;
(2)代数式m2+3的最小值是____3;
(探究):求代数式n2+4n+9的最小值,小明是这样做的:
n2+4n+9
=n2+4n+4+5
=(n+2)2+5
∴当n=-2时,代数式n2+4n+9有最小值,最小值为5.
请你参照小明的方法,求代数式a2-6a-3的最小值,并求此时a的值.
(拓展):(3)代数式m2+n2-8m+2n+17=0,求m+n的值.
(4)若y=-4t2+12t+6,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
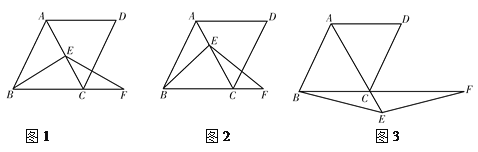
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com