
【题目】如图,已知抛物线的方程y=- ![]() (x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
(x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
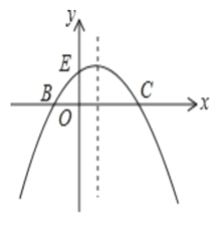
(1)求该抛物线的解析式
(2)在(1)的条件下,求△BCE的面积
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使EH+BH的值最小。求出点H的坐标。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接带入P点坐标求出m即可;(2)由(1)求出的函数关系式,解出函数与x,y轴的交点坐标,即可求出三角形面积;(3)作E关于抛物线对称轴的对称点F,连接BF交y轴于点H,由两点之间线段最短可得最小值。
(1)解:将P点代入函数式得:![]()
解得: m=4,
∴ 该抛物线的解析式为: ![]() .
.
(2)解: 由(1)得-![]() (x+2)(x-4)=0,
(x+2)(x-4)=0,
解得x=-2或x=4,
∴B(-2,0),C(4,0),
∴BC=4-(-2)=6,
当x=0, y=2,
∴OE=2.
∴![]()
(3)解: 如图,作E关于抛物线对称轴的对称点F,连接BF交y轴于点H,
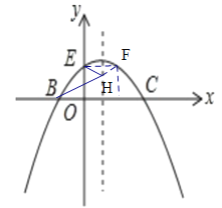
∵![]() ,
,
则F(2,2),
EH+BH=FH+HB=FB,
设直线FB的解析式为:y=kx+b,
∴![]()
解得: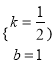 ,
,
故y=![]() ,
,
当x=1, y=![]() ×1+1=
×1+1=![]() ,
,
∴H(1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 且
且![]() )的图象在第一象限交于点
)的图象在第一象限交于点![]() 、
、![]() ,且该一次函数的图象与
,且该一次函数的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .已知
.已知![]() ,
,![]() .
.
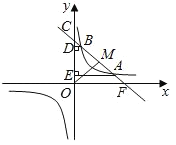
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)若点![]() 为一次函数图象上的动点,求
为一次函数图象上的动点,求![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
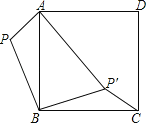
A.105° B.112.5° C.120° D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
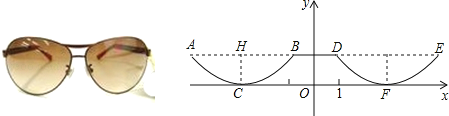
【题目】如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=![]() (x+3)2
(x+3)2
B.y=![]() (x+3)2
(x+3)2
C.y=![]() (x﹣3)2
(x﹣3)2
D.y=![]() (x﹣3)2
(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,其他三边用总长为60米栅栏围住(如图),若设绿化带的BC边为x米,绿化带的面积为y平方米。

(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围:
(2)是否存在绿化带BC的长的某个值,使得绿化带的面积为450平方米?若存在,请求出这个值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
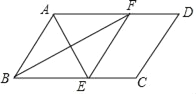
【题目】如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,移动电商发展迅速,以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题:

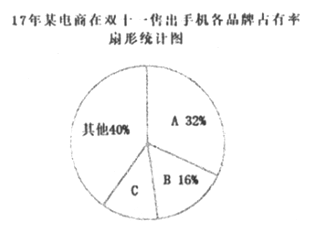
(1)2017年10月“移动电商行业用户规模”是___________亿台(结果精确到0.1亿台);并补全条形统计图;
(2)2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台,若按此平均数增长,请你估计2018年1月“移动电商行业用户规模”为___________亿台(结果精确到0.1亿台);
(3)2017年某电商在双十一共售出手机12000台,则C品牌手机售出的台数是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校进行校园美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,如果由甲队先做20天,剩下的工程由甲、乙合作24天完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需要支付工程款3.5万元,乙队施工一天需要支付工程款2万元:如果规定在70天内完成这项工作,是由甲、乙两队单独完成省钱?还是由甲乙合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是(____)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com