
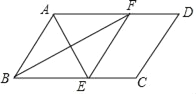
【题目】如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
【答案】(1)证明见解析;(2)BC=3+3![]() .
.
【解析】
(1)首先证明四边形ABEF是平行四边形,再由平行线的性质和角平分线证出∠BAE=∠AEB,证出AB=EB,得出四边形ABEF是菱形,即可得出结论;
(2)由相似多边形的性质得出对应边成比例,即可得出BC的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴![]() ,即
,即![]() ,
,
解得:BC=3±3![]() (负值舍去),
(负值舍去),
∴BC=3+3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
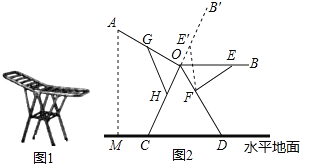
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的方程y=- ![]() (x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
(x+2)(x-m) (m>0)与x轴交于B、C,与y轴交于点E,且点B在点C的左侧,抛物线还经过点P(2,2)
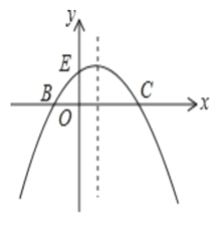
(1)求该抛物线的解析式
(2)在(1)的条件下,求△BCE的面积
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使EH+BH的值最小。求出点H的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O 的内接△ABC 中,∠ABC=30°,AC 的延长线与过点 B 的⊙O 的切线相交于点 D,若⊙O 的半径 OC=1,BD∥OC,则 CD 的长为( )
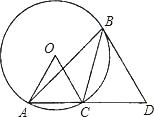
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位宿舍用电规定如下:如果每户一个月的用电量不超过![]() 度,那么这个月只需要交10元电费,若超过
度,那么这个月只需要交10元电费,若超过![]() 度,则这个月除了要交10元电费外,超过的部分还要按
度,则这个月除了要交10元电费外,超过的部分还要按![]() 元交费,下表是某户5月份和6月份的用电和交费情况,求
元交费,下表是某户5月份和6月份的用电和交费情况,求![]() 的值.
的值.
月份 | 用电量(度) | 交电费总数(元) |
5 | 80 | 25 |
6 | 45 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com