
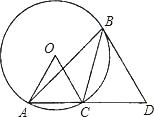
【题目】如图,在⊙O 的内接△ABC 中,∠ABC=30°,AC 的延长线与过点 B 的⊙O 的切线相交于点 D,若⊙O 的半径 OC=1,BD∥OC,则 CD 的长为( )
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作辅助线OB、CE构建正方形CEBO.根据圆周角定理(同弧所对的圆周角是所对的圆心角的一半)求得∠OAC=2∠ABC=60°,然后由切线的性质及平行线的性质求得OB⊥OC,OB⊥BD;再根据圆的半径都相等知OB=OC,所以判定四边形CEBO是正方形,然后在直角三角形CDE中利用正弦三角函数sin∠D=sin60°求CD的长度并作出选择.
连接OB,过点C作CE⊥BD于点E,
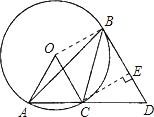
∵∠ABC=30°,
∴∠AOC=60°(同弧所对的圆周角是所对的圆心角的一半);
∵OA=OC(⊙O的半径),
∴∠ACO=∠OAC=60°(等边对等角),
又BD∥OC,
∴∠ACO=∠D=60°(两直线平行,同位角相等),
∴∠OCD=120°(两直线平行,同旁内角互补),
∵BD是⊙O的切线,
∴OB⊥OC,OB⊥BD,
又∵OB=OC,
∴四边形CEBO是正方形,
∴CE=OB=1,
∴CD=![]() =
=![]() ,
,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7 及以上 |
人数(人) | 10 | 14 | m | 8 | 6 |
请根据统计图表中的信息,解答下列问题:
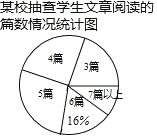
(1)求被抽查的学生人数和 m 的值;
(2) 求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有 1200 名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为 4 篇的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是![]() 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖
D. 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com