
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ�� 40 Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ����� 80 Ԫ�����г����飬ÿ��������� y�� ǧ������ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ���������������

��1���� y �� x ֮��ĺ�������ʽ��
��2������Ʒÿ���������Ϊ W��Ԫ������ W �� x ֮��ĺ�������ʽ�����������멁�ɱ�����
��3��ָ���ۼ�Ϊ����Ԫʱ������������˵����2����������W���ۼ�x�ı仯���仯�������
���𰸡���1��y����2x+200��40��x��80������2��W����2x2+280x��8000����3���ۼ�Ϊ 70 Ԫʱ������������������� 1800 Ԫ��
��������
��1������ϵ�������ɵã�(2)������������ÿǧ�����������������ɵú�������ʽ��(3)�� w �� x �ĺ�����ϵʽ�䷽�ɶ���ʽ���ɵ���ֵ�����
��1���� y��kx+b��
����50��100������60��80�����룬�ã�![]() ��
��
��ã�![]() ��
��
��y����2x+200 ��40��x��80����
��2��W����x��40������2x+200��
����2x+280x��8000��
W �� x ֮��ĺ�������ʽΪ W����2x+280x��8000��
��3��W����2x+280x��8000
����2(x��70)+1800��
�൱ x��70 ʱ��W ȡ�����ֵΪ 1800��
���ۼ�Ϊ 70 Ԫʱ������������������� 1800 Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���������ſ�Ƭ����Ϸ����Ƭ�Ϸֱ�д��A��B��B����Щ��Ƭ����ĸ����ȫ��ͬ�������������һ�ţ�������ĸ��Żأ����ϴ�Ⱥ��ٴ�������һ�ţ��������������Ƭ��ĸ��ͬ��С��ʤ������С��ʤ�������Ϸ��˫����ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
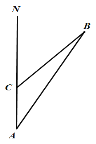
����Ŀ�����㵺�Թ��������ҹ��Ĺ����������������ǹ����ۺϹ�����ǿʢ�����ҶԵ��㵺��Ѳ���ѳ�̬����2017��9��11�գ��й�����2401�Ŵ���A�ز�õ��㵺B�ڱ�ƫ��30�㷽���ָú�����������A�س�����30����/Сʱ���ٶ�������������2Сʱ��C�أ�
(1)����B=15�㣬����㵺B��C�صı�ƫ�����ٶȣ�
(2)��(1)�Ļ����ϣ���������㵺�ľ���CB�ij���������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A��110����E��F�ֱ��DZ�AB��BC���е㣬EP��CD�ڵ�P�����PEF����������
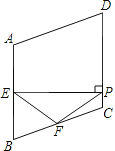
A.35��B.45��C.50��D.55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��4��0����B��0��2����C��4��4������֪�ı���ABCDΪ���Σ�����AB��BCΪһ���ڱߣ�
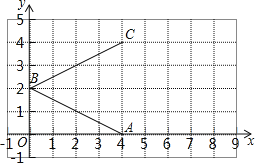
��1������ͼ����������ABCD�����������ABCD�������
��2������A��ֱ��l��y��![]() x+b���߶�CD�ཻ�ڵ�E������ͼ������ֱ��l��ͼ�������ADE�������
x+b���߶�CD�ཻ�ڵ�E������ͼ������ֱ��l��ͼ�������ADE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
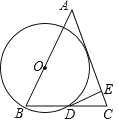
����Ŀ����ͼ������O ���ڽ���ABC ������ABC��30�㣬AC ���ӳ�������� B ����O �������ཻ�ڵ� D������O �İ뾶 OC��1��BD��OC���� CD �ij�Ϊ�� ��
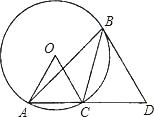
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� O ����ABC �ı� AB ��һ�㣬�� OB Ϊ�뾶����O �� BC �ڵ� D������ D �����߽� AC �ڵ� E���� DE��AC��
(1)֤����AB��AC��
(2)�� AB��![]() cm��BC��2cm������ O �� AB ���ƶ���ʹ��O ��� AC ����ֱ������ʱ�� ����O �İ뾶��
cm��BC��2cm������ O �� AB ���ƶ���ʹ��O ��� AC ����ֱ������ʱ�� ����O �İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
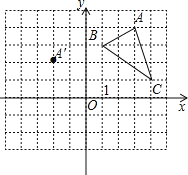
����Ŀ����ƽ��ֱ������ϵ�У�������![]() �����������λ����ͼ��ʾ��
�����������λ����ͼ��ʾ��![]() ��������
��������![]() ���ֽ�������
���ֽ�������![]() ƽ�ƣ�ʹ��
ƽ�ƣ�ʹ��![]() �任Ϊ��
�任Ϊ��![]() ����
����![]() �ֱ���
�ֱ���![]() �Ķ�Ӧ��
�Ķ�Ӧ��
![]() �뻭��ƽ�ƺ��������
�뻭��ƽ�ƺ��������![]() (��д����)��ֱ��д����B'�����꣺
(��д����)��ֱ��д����B'�����꣺![]()
![]() ��������
��������![]() �ڲ�һ��
�ڲ�һ��![]() ������Ϊ
������Ϊ![]() �����
�����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ��������
��������
![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() ��
��![]() ���ڵ�ֱ���ϣ���
���ڵ�ֱ���ϣ���![]() ������
������![]() �ϣ���
�ϣ���![]() ������
������![]() ��
��
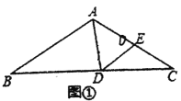
��1����ͼ�٣���![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
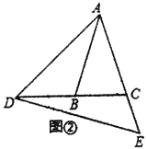
��2����ͼ�ڣ���![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
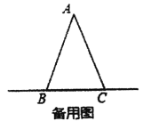
��3������![]() ��ֱ��
��ֱ��![]() ��(�����
��(�����![]() ��
��![]() �غ�)�˶�ʱ����̽��
�غ�)�˶�ʱ����̽��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com