
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
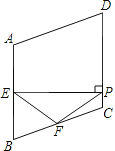
A.35°B.45°C.50°D.55°
【答案】A
【解析】
延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数,根据余角的定义即可得到结果.
解:延长PF交AB的延长线于点G.
在△BGF与△CPF中,
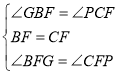 ,
,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点,
又∵∠BEP=90°,
∴EF=![]() PG(直角三角形斜边上的中线等于斜边的一半),
PG(直角三角形斜边上的中线等于斜边的一半),
∵PF=![]() PG(中点定义),
PG(中点定义),
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP﹣∠FEP=∠EPC﹣∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°﹣∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=![]() (180°﹣70°)=55°,
(180°﹣70°)=55°,
∴∠FPC=55°,
∴∠EPF=35°,
∵EF=PF,
∴∠PEF=∠EPF=35°,
故选:A.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假丽丽用一块边长为10的正方形彩纸为她的人偶玩具做了一件披风,如图所示,先将正方形纸片![]() 对折,展平后得到中线
对折,展平后得到中线![]() ,再分别沿折痕
,再分别沿折痕![]() ,
,![]() 将点
将点![]() ,点
,点![]() 都折到
都折到![]() 上点
上点![]() 处,此时领口
处,此时领口![]() 的长为( )
的长为( )
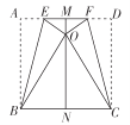
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是![]() 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖
D. 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com