
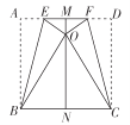
【题目】寒假丽丽用一块边长为10的正方形彩纸为她的人偶玩具做了一件披风,如图所示,先将正方形纸片![]() 对折,展平后得到中线
对折,展平后得到中线![]() ,再分别沿折痕
,再分别沿折痕![]() ,
,![]() 将点
将点![]() ,点
,点![]() 都折到
都折到![]() 上点
上点![]() 处,此时领口
处,此时领口![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
科目:初中数学 来源: 题型:
【题目】已知![]() 为原点,点
为原点,点![]() 及在第一象限的动点
及在第一象限的动点![]() ,且
,且![]() ,设
,设![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(4)画出函数![]() 的图象.
的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
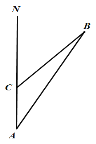
【题目】钓鱼岛自古以来是我国的固有领土,随着我们国家综合国力的强盛,国家对钓鱼岛的巡航已常态化.2017年9月11日,中国海警2401号船在A地测得钓鱼岛B在北偏东30°方向,现该海警船继续从A地出发以30海里/小时的速度向正北方向航行2小时后到达C地.
(1)若∠B=15°,求钓鱼岛B在C地的北偏东多少度?
(2)在(1)的基础上,求海警船与钓鱼岛的距离CB的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
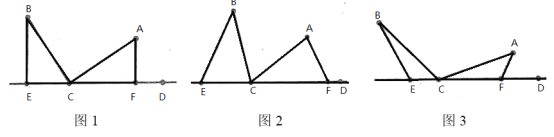
【题目】直线CD是经过∠BCA顶点C的一条直线,CA=CB,点E、F分别是直线CD上的两点,且∠BEC=∠CFA=∠BCA,
(1)如图1,当∠BCA=90时,则BE与CF的数量关系是:______________
(2)如图2,当∠BCA为锐角时,(1)中的数量关系是否依然成立?若成立,请证明
(3)如图 3,当∠BCA为钝角时,请说出EF、BE、AF三条线段的数量关系(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
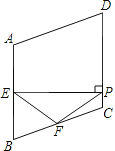
A.35°B.45°C.50°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(4,0),B(0,2),C(4,4).已知四边形ABCD为菱形,其中AB与BC为一组邻边.
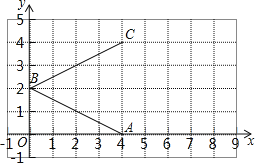
(1)请在图中作出菱形ABCD,并求出菱形ABCD的面积;
(2)过点A的直线l:y=![]() x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.
x+b与线段CD相交于点E,请在图中作出直线l的图象,并求出△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
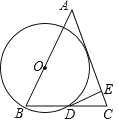
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数的图象交坐标轴于 A(﹣1,0),B(4,0),C
(0,﹣4)三点,点 P 是直线 BC 下方抛物线上一动点.
(1) 求这个二次函数的解析式;
(2) 是否存在点 P,使△POC 是以 OC 为底边的等腰三角形?若存在,求出 P 点坐标;若不存在,请说明理由;
(3) 在抛物线上是否存在点 D(与点 A 不重合)使得 S△DBC=S△ABC,若存在,求出点 D的坐标;若不存在,请说明理由.
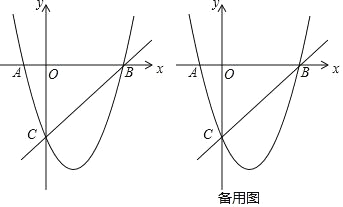
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com