
����Ŀ����ƽ��ֱ������ϵ�У����κ�����ͼ���������� A����1��0����B��4��0����C
��0����4�����㣬�� P ��ֱ�� BC �·���������һ���㣮
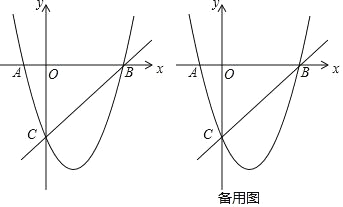
��1�� ��������κ����Ľ���ʽ��
��2�� �Ƿ���ڵ� P��ʹ��POC ���� OC Ϊ�ױߵĵ��������Σ������ڣ���� P �����ꣻ�������ڣ���˵�����ɣ�
��3�� �����������Ƿ���ڵ� D����� A ���غϣ�ʹ�� S��DBC��S��ABC�������ڣ������ D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)�����߽���ʽΪy��x2��3x��4��(2)��������������P�㣬������Ϊ��![]() ����2����(3)��������������D�㣬������Ϊ��5��6����
����2����(3)��������������D�㣬������Ϊ��5��6����
��������
��1����A��B��C��������꣬���ô���ϵ��������������߽���ʽ��
��2���������֪��P���߶�OC�Ĵ�ֱƽ�����ϣ�������P�������꣬���������߽���ʽ�����P�����ꣻ
��3�����ڣ�������������ۣ������ô���ϵ�����Լ��ⷽ���鼴�ɽ�����⣮
(1)�������߽���ʽΪy��ax2+bx+c��
��A��B��C�����������ɵ�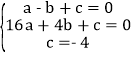 �����
�����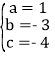 ��
��
�������߽���ʽΪy��x2��3x��4��
(2)��ͼ1����OC�Ĵ�ֱƽ����DP����OC�ڵ�D����BC�·��������ڵ�P��
��PO��PC����ʱP�㼴Ϊ���������ĵ㣬
��C��0����4����
��D��0����2����
��P����������2��
���������߽���ʽ�ɵ�x2��3x��4����2�����x��![]() ��С��0����ȥ����x��
��С��0����ȥ����x��![]() ��
��
���������������P�㣬������Ϊ��![]() ����2����
����2����
(3)��ͼ2��
�ٵ�D����ֱ��BC���Ϸ�ʱ����A����AD1��BC������������D1����ʱ��ʹ��S��DBC��S��ABC��
��B��4��0����C��0����4����
��ֱ��BC�Ľ���ʽΪy��x��4��
��AD1��BC��
����ֱ��AD11�Ľ���ʽΪy��x+n��
��A����1��0������ã�0����1+n����n��1��
��ֱ��AD1�Ľ���ʽΪy��x+1��
��![]() ��
��![]() ��
��![]() ��
��
��D1��������5��6����
�ڵ�D����ֱ��BC���·�ʱ��
��ֱ��AD1�Ľ���ʽΪy��x+1��ֱ֪��AD1��y��Ľ���E������Ϊ��0�� 1����
��CE��5��
��ֱ��AD�Ľ���ʽΪy��x��10��
�߷���x2��3x��4��x��10��ʵ������
�ʴ�������������D�㣬������Ϊ��5��6����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ��߳�Ϊ10�������β�ֽΪ������ż�������һ�����磬��ͼ��ʾ���Ƚ�������ֽƬ![]() ���ۣ�չƽ��õ�����
���ۣ�չƽ��õ�����![]() ���ٷֱ����ۺ�
���ٷֱ����ۺ�![]() ��
��![]() ����
����![]() ����
����![]() ���۵�
���۵�![]() �ϵ�
�ϵ�![]() ������ʱ���
������ʱ���![]() �ij�Ϊ�� ��
�ij��� ��
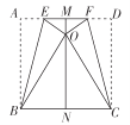
A.![]() B.
B.![]() C.3D.
C.3D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ſ�����ȵ�ֽ��������һ���ص����ֹ����ı���ABCD��
��1����֤���ı���ABCD�����Σ�
��2����ֽ����3cm����ABC=60�������ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С��һ�ҳ�������ǰ��ij�����Σ��ƻ��ڶ�����������Դ�����Լݳ��Ρ�
 [��
[��
����������Ϣ������������⣺
��1�����ʱ��Ϊ![]() Сʱ�����ü�˾�ij��������Ϊ
Сʱ�����ü�˾�ij��������Ϊ![]() Ԫ�������ҹ�˾�ij��������Ϊ
Ԫ�������ҹ�˾�ij��������Ϊ![]() Ԫ���ֱ����
Ԫ���ֱ����![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������С�����㲢ѡ���ĸ����η������㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
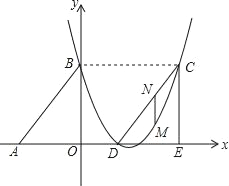
����Ŀ����ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B������������Ϊ����3��0������0��4����������y��![]() x2+bx+c����B�㣬�Ҷ�����ֱ��y��
x2+bx+c����B�㣬�Ҷ�����ֱ��y��![]() �ϣ�
�ϣ�
(1)�������߶�Ӧ�ĺ�����ϵʽ��
(2)����DCE���ɡ�ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
(3)��(2)�������£���M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊs����s��t֮��ĺ�����ϵʽ��д���Ա���t��ȡֵ��Χ������sȡ��ֵʱ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�OΪ����ԭ�㣬A��1��1������x����ȷ����P��ʹ��AOPΪ���������Σ�����������ĵ�P�ĸ������У� ��
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
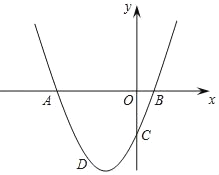
����Ŀ����֪��������y��ax2+2ax+c��y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ��1��0����OC��3OB��
��1���������ߵĽ���ʽ��
��2����a��0ʱ����ͼ��ʾ������D�ǵ��������������ϵĶ��㣬���D�ĺ�����Ϊm��������ADC�����ΪS�����S��m�ĺ�����ϵʽ����ֱ��д���Ա���m��ȡֵ��Χ�����ʵ�mΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����![]() +bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
+bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
(1)����κ����ı���ʽ��
(2)��ͼ1����D�������ߵ��������ϵ�һ���㣬����DC��DB����S��DCB��S��ABCʱ�����D���ꣻ
(3)��ͼ2����(2)�������£���Q��CA���ӳ����ϣ�����DQ��AD������Q��QP��y�ᣬ����������P������AQD����ACO+��ADC�������PQ�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A=90����O��BC����һ�㣬��OΪԲ�ĵİ�Բ��AB�������ڵ�D����AC��BC�߷ֱ��ڵ�E��F��G������OD����֪BD=2��AE=3��tan��BOD=![]() ��
��
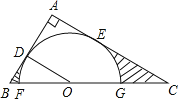
��1������O�İ뾶OD��
��2����֤��AE����O�����ߣ�
��3����ͼ����������Ӱ����ĺͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com