
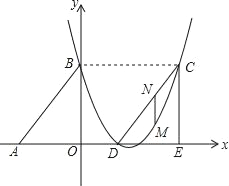
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=![]() x2+bx+c经过B点,且顶点在直线y=
x2+bx+c经过B点,且顶点在直线y=![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由.
(3)在(2)的条件下,若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为s,求s与t之间的函数关系式,写出自变量t的取值范围,并求s取大值时,点M的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+4;(2)点C和点D在所求抛物线上;(3)s=﹣
x+4;(2)点C和点D在所求抛物线上;(3)s=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,当s最大时,此时点M的坐标为(
,当s最大时,此时点M的坐标为(![]() ,
,![]() ).
).
【解析】
(1)已知了抛物线上A、B点的坐标以及抛物线的对称轴方程,可用待定系数法求出抛物线的解析式.
(2)首先求出AB的长,将A、B的坐标向右平移AB个单位,即可得出C、D的坐标,再代入抛物线的解析式中进行验证即可.
(3)根据C、D的坐标,易求得直线CD的解析式;那么线段MN的长实际是直线BC与抛物线的函数值的差,可将x=t代入两个函数的解析式中,得出的两函数值的差即为l的表达式,由此可求出l、t的函数关系式,根据所得函数的性质即可求出l取最大值时,点M的坐标.
(1)∵y=![]() x2+bx+c的顶点在直线x=
x2+bx+c的顶点在直线x=![]() 上,
上,
∴可设所求抛物线对应的函数关系式为y=![]() (x﹣
(x﹣![]() )2+m,
)2+m,
∵点B(0,4)在此抛物线上,
∴4=![]() (0﹣
(0﹣![]() )2+m,
)2+m,
∴m=﹣![]() ,
,
∴所求函数关系式为:y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() =
=![]() x2﹣
x2﹣![]() x+4;
x+4;
(2)在Rt△ABO中,OA=3,OB=4,
∴AB=![]() =5.
=5.
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5,
∵A、B两点的坐标分别为(﹣3,0))、(0,4),
∴C、D两点的坐标分别是(5,4)、(2,0);
当x=5时,y=![]() ×52﹣
×52﹣![]() ×5+4=4,
×5+4=4,
当x=2时,y=![]() ×22﹣
×22﹣![]() ×2+4=0,
×2+4=0,
∴点C和点D在所求抛物线上;
(3)设直线CD对应的函数关系式为y=kx+n,
则![]() ,
,
解得: ;
;
∴y=![]() x﹣
x﹣![]() .
.
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t;
则yM=![]() t2﹣
t2﹣![]() t+4,yN=
t+4,yN=![]() t﹣
t﹣![]() ,
,
∴s=yN﹣yM=(![]() t﹣
t﹣![]() )﹣(
)﹣(![]() t2﹣
t2﹣![]() t+4)
t+4)
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当t=![]() 时,s最大=
时,s最大=![]() ,此时yM=
,此时yM=![]() ×(
×(![]() )2﹣
)2﹣![]() ×
×![]() +4=
+4=![]() .
.
此时点M的坐标为(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
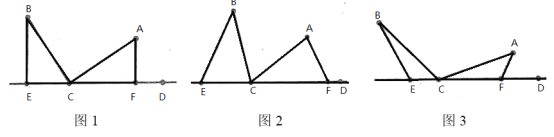
【题目】直线CD是经过∠BCA顶点C的一条直线,CA=CB,点E、F分别是直线CD上的两点,且∠BEC=∠CFA=∠BCA,
(1)如图1,当∠BCA=90时,则BE与CF的数量关系是:______________
(2)如图2,当∠BCA为锐角时,(1)中的数量关系是否依然成立?若成立,请证明
(3)如图 3,当∠BCA为钝角时,请说出EF、BE、AF三条线段的数量关系(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要招聘甲、乙两种工种的工人![]() 人,甲、乙两种工种的工人的月工资分别为
人,甲、乙两种工种的工人的月工资分别为![]() 元和
元和![]() 元
元
![]() 设招聘甲种工种工人
设招聘甲种工种工人![]() 人,工厂付给用、乙两种工种的工人工资共
人,工厂付给用、乙两种工种的工人工资共![]() 元,写出
元,写出![]() (元)与
(元)与![]() (人)的函数关系式;
(人)的函数关系式;
![]() 现要求招聘的乙种工种的人数不少于甲种工种人数的
现要求招聘的乙种工种的人数不少于甲种工种人数的![]() 倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
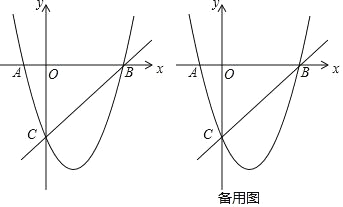
【题目】在平面直角坐标系中,二次函数的图象交坐标轴于 A(﹣1,0),B(4,0),C
(0,﹣4)三点,点 P 是直线 BC 下方抛物线上一动点.
(1) 求这个二次函数的解析式;
(2) 是否存在点 P,使△POC 是以 OC 为底边的等腰三角形?若存在,求出 P 点坐标;若不存在,请说明理由;
(3) 在抛物线上是否存在点 D(与点 A 不重合)使得 S△DBC=S△ABC,若存在,求出点 D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
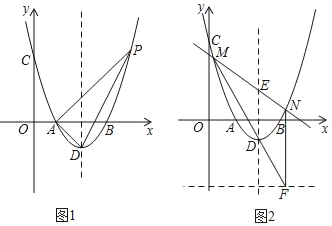
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
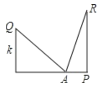
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
A.hB.kC.aD.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com