【题目】如图，点D，E分别在等边△ABC的边AB，BC上，将△BDE沿直线DE翻折，使点B落在B1处．若∠ADB1=70°，则∠CEB1=___．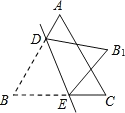
【答案】50°
【解析】
由等边三角形的性质可知：∠B=60°，由邻补角的定义可知∠BDB1=110°，然后由翻折的性质可求得∠BDE=55°，△BDE中由三角形的内角和定理可求得∠BED=65°，然后由翻折的性质可知∠BEB1=130°，从而可求得∠CEB1=50°．
由翻折的性质可知：∠BDE=∠B1DE，
∵∠ADB1=70°，
∴∠BDB1=110°，∴∠BDE=
∠BDB1=×110°=55°，
∵△ABC为等边三角形，
∴∠B=60°．
在△BDE中，∠BED=180°-55°-60°=65°．
由翻折的性质可知：∠BEB1=2×65°=130°
∴∠CEB1=180°-130°=50°．
故答案为：50°．
科目：初中数学 来源： 题型：
【题目】如图，一艘轮船航行到 B 处时，测得小岛 A 在船的北偏东 60°的方向，轮船从 B 处继续向正东方向航行 20 海里到达 C 处时，测得小岛 A 在北船的北偏东 30°的方向．
（1）若小岛 A 到这艘轮船航行路线 BC 的距离是 AD，求 AD 的长．
（2）已知在小岛周围 17 海里内有暗礁，若轮船不改变航向继续向前行驶，试问轮船有无触礁的危险？（
≈1.732）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一类随机事件概率的计算方法：设试验结果落在某个区域S中的每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A）=
． 有一块边长为30cm的正方形ABCD飞镖游戏板，假设飞镖投在游戏板上的每一点的机会均等．求下列事件发生的概率：
(1)在飞镖游戏板上画有半径为5cm的一个圆（如图1），求飞镖落在圆内的概率；
(2)飞镖在游戏板上的落点记为点O，求△OAB为钝角三角形的概率．
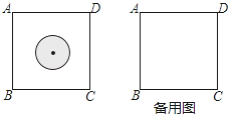
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（﹣3，0）、（0，4），抛物线y＝
x2+bx+c经过B点，且顶点在直线y＝
上．
(1)求抛物线对应的函数关系式；
(2)若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由．
(3)在(2)的条件下，若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为s，求s与t之间的函数关系式，写出自变量t的取值范围，并求s取大值时，点M的坐标．
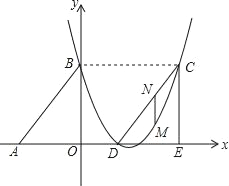
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，抛物线y＝ax2+2ax+c与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC＝3OB．
（1）求抛物线的解析式；
（2）当a＞0时，如图所示，若点D是第三象限方抛物线上的动点，设点D的横坐标为m，三角形ADC的面积为S，求出S与m的函数关系式，并直接写出自变量m的取值范围；请问当m为何值时，S有最大值？最大值是多少．
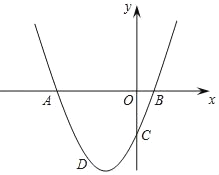
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+2x+c与x轴交A（﹣1，0），B两点，与y轴交于点C（0，3），抛物线的顶点为点E．
(1)求抛物线的解析式；
(2)经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一个动点，当点P运动到点E时，求△PCD的面积；
(3)点N在抛物线对称轴上，点M在x轴上，是否存在这样的点M与点N，使以M，N，C，B为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标（不写求解过程）；若不存在，请说明理由．
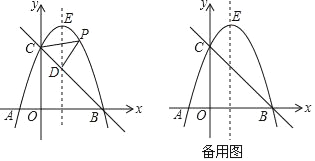
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF=4，则下列结论：①
；②S△BCE=36；③S△ABE=12；④△AEF～△ACD，其中一定正确的是（ ）
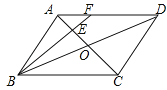
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，平面直角坐标系中，直线 y1=x+3与抛物线y2=﹣
+2x 的图象如图，点P是 y2 上的一个动点，则点P到直线 y1 的最短距离为（）
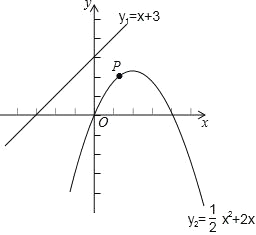
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
