
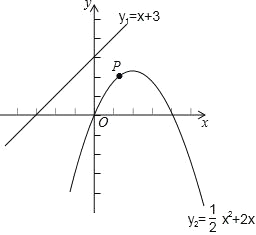
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
设过点P平行直线y1的解析式为y=x+b,当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,
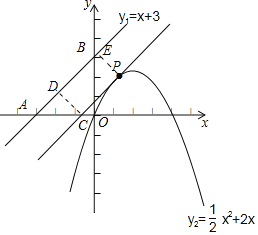
由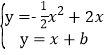 ,消去y得到:x2-2x+2b=0,
,消去y得到:x2-2x+2b=0,
当△=0时,4-8b=0,
∴b=![]() ,
,
∴直线的解析式为y=x+![]() ,
,
如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-
交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-![]() ,0),
,0),
∴OA=OB=3,OC=![]() ,AC=
,AC=![]() ,
,
∴∠DAC=45°,
∴CD=![]() =
=![]() ,
,
∵AB∥PC,CD⊥AB,PE⊥AB,
∴PE=CD=![]() ,
,
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+3经过点A(﹣1,8),顶点为M;
(1)求抛物线的表达式;
(2)设抛物线对称轴与x轴交于点B,连接AB、AM,求△ABM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
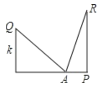
A.hB.kC.aD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
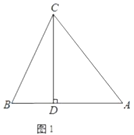
【题目】如图1,![]() 中,
中,![]() 于
于![]() ,且
,且![]() .
.
(1)试说明![]() 是等腰三角形;
是等腰三角形;
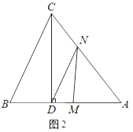
(2)已知![]() ,如图2,动点
,如图2,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,设点
运动,设点![]() 运动的时间为
运动的时间为![]() (秒)
(秒)![]() .
.
①若![]() 的边于
的边于![]() 平行,求
平行,求![]() 的值;
的值;
②若点![]() 是边
是边![]() 的中点,问在点
的中点,问在点![]() 运动的过程中,
运动的过程中,![]() 能否成为等腰三角形?若能,求出
能否成为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
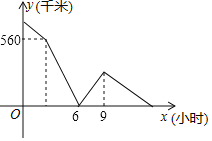
【题目】A、B、C三地在同一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
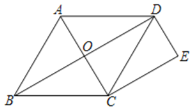
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=3时,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com