
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃНЉ![]() x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЖўДЮКЏЪ§yЃНЉ
x+2гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЖўДЮКЏЪ§yЃНЉ![]() +bx+cЕФЭМЯѓОЙ§BЃЌCСНЕуЃЌЧвгыxжсЕФИКАыжсНЛгкЕуAЃЎ
+bx+cЕФЭМЯѓОЙ§BЃЌCСНЕуЃЌЧвгыxжсЕФИКАыжсНЛгкЕуAЃЎ
(1)ЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)ШчЭМ1ЃЌЕуDЪЧХзЮяЯпЕкЫФЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгDCЃЌDBЃЌЕБSЁїDCBЃНSЁїABCЪБЃЌЧѓЕуDзјБъЃЛ
(3)ШчЭМ2ЃЌдк(2)ЕФЬѕМўЯТЃЌЕуQдкCAЕФбгГЄЯпЩЯЃЌСЌНгDQЃЌADЃЌЙ§ЕуQзїQPЁЮyжсЃЌНЛХзЮяЯпгкPЃЌШєЁЯAQDЃНЁЯACO+ЁЯADCЃЌЧыЧѓГіPQЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ6
ЃЛЃЈ3ЃЉ6
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіBЁЂCЕФзјБъЃЌШЛКѓДњШыЖўДЮКЏЪ§ЕФНтЮіЪНЃЌНтЗНГЬзщМДПЩЃЛ
(2)Й§DзїDGЁЭxжсгкGЃЌЙ§CзїCFЁЭDGгкFЃЌЙ§BзїBEЁЭCFгкEЃЎЩшDЃЈxЃЌyЃЉЃЌдђxЃО0ЃЌyЃМ0ЃЎЧѓГіSЁїABCЃЎИљОнSЁїCBD=SЁїCDFЃSЁїCEBЃSЬнаЮEBDFНтЗНГЬНтЕУЕНxЕФжЕЃЌДгЖјЕУЕНDЕФзјБъЃЛ
(3)СЌНгADЃЌЙ§DзїDMЁЭxжсгкMЃЎЯШЧѓГіжБЯпCDЕФНтЮіЪНЮЊy=Ѓx+2ЃЌЕУЕНCO=OR=2ЃЌдђЁЯORC=45ЁуЃЎдйжЄУїЁЯAQD=45ЁуЃЎЭЈЙ§ЙДЙЩЖЈРэЕФФцЖЈРэЕУЕНAC2+AD2= DC2ЃЌМДгаЁЯCAD=90ЁуЃЌДгЖјгаЁїAQDЪЧЕШбќжБНЧШ§НЧаЮЃЌгЩЕШбќШ§НЧаЮЕФаджЪЕУЕНAQ=ADЃЎЭЈЙ§жЄУїЁїQANЁеЁїADMЃЌЕУЕНNAЃЌQNЕФГЄЃЌНјЖјЕУЕНON=4ЃЌМДПЩЕУЕНNЃЈЃ4ЃЌ0ЃЉЃЌдђPЕуКсзјБъЮЊx=-4ЃЌДњШыЖўДЮКЏЪ§МДПЩЕУЕНyЕФжЕЃЌДгЖјЕУЕННсТлЃЎ
ЃЈ1ЃЉдк![]() жаЃЌСюy=0ЃЌНтЕУЃКx=4ЃЌЁрB(4ЃЌ0)ЃЌСюx=0ЃЌЕУЃКy=2ЃЌЁрC(0ЃЌ2)ЃЎАбB(4ЃЌ0)ЃЌC(0ЃЌ2)ДњШы
жаЃЌСюy=0ЃЌНтЕУЃКx=4ЃЌЁрB(4ЃЌ0)ЃЌСюx=0ЃЌЕУЃКy=2ЃЌЁрC(0ЃЌ2)ЃЎАбB(4ЃЌ0)ЃЌC(0ЃЌ2)ДњШы![]() жаЃЌЕУЃК
жаЃЌЕУЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁрЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃК
ЃЌЁрЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃК![]() ЃЎ
ЃЎ
(2)Й§DзїDGЁЭxжсгкGЃЌЙ§CзїCFЁЭDGгкFЃЌЙ§BзїBEЁЭCFгкEЃЎЩшDЃЈxЃЌyЃЉЃЎ
ЁпDдкЕкЫФЯѓЯоЃЌЁрxЃО0ЃЌyЃМ0ЃЎ
ЁпBЃЈ4ЃЌ0ЃЉЃЌC(0ЃЌ2)ЃЌЁрCE=OB=4ЃЌCO=BE=FG=2ЃЌEF=BG=x-4ЃЌDF=DG+FG=2-yЃЌSЁїABC=![]() ABЁСOC=
ABЁСOC=![]() ЁСЃЈ4+1ЃЉЁС2=5ЃЎ
ЁСЃЈ4+1ЃЉЁС2=5ЃЎ
SЁїCBD=SЁїCDFЃSЁїCEBЃSЬнаЮEBDF=![]() ЃЌЛЏМђЕУЃКx+2y=Ѓ1ЃЎ
ЃЌЛЏМђЕУЃКx+2y=Ѓ1ЃЎ
ЁпDЃЈxЃЌyЃЉдкЖўДЮКЏЪ§![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌЛЏМђЕУЃК
ЃЌЛЏМђЕУЃК![]() ЃЌЁрЃЈxЃ5ЃЉЃЈx+1ЃЉ=0ЃЌЁрx=5Лђx=Ѓ1ЃЈЩсШЅЃЉЃЎ
ЃЌЁрЃЈxЃ5ЃЉЃЈx+1ЃЉ=0ЃЌЁрx=5Лђx=Ѓ1ЃЈЩсШЅЃЉЃЎ
ЕБx=5ЪБЃЌy=![]() =Ѓ3ЃЌЁрDЃЈ5ЃЌЃ3ЃЉЃЎ
=Ѓ3ЃЌЁрDЃЈ5ЃЌЃ3ЃЉЃЎ

(3)ШчЭМЃЌСЌНгADЃЌЙ§DзїDMЁЭxжсгкMЃЎЩшжБЯпCDЕФНтЮіЪНЮЊy=kx+bЃЌАбCЃЈ0ЃЌ2ЃЉЃЌDЃЈ5ЃЌЃ3ЃЉДњШыЕУЕНЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁржБЯпCDЕФНтЮіЪНЮЊy=Ѓx+2ЃЌСюy=0ЃЌНтЕУЃКx=2ЃЌЁрR(2ЃЌ0)ЃЌЁрCO=OR=2ЃЌЁрЁЯORC=45ЁуЃЎ
ЃЌЁржБЯпCDЕФНтЮіЪНЮЊy=Ѓx+2ЃЌСюy=0ЃЌНтЕУЃКx=2ЃЌЁрR(2ЃЌ0)ЃЌЁрCO=OR=2ЃЌЁрЁЯORC=45ЁуЃЎ
ЁпЁЯACO+ЁЯCAO=90ЁуЃЌЁЯCAO+ЁЯOAD=90ЁуЃЌЁрЁЯACO=ЁЯOADЃЌЁрЁЯACO+ЁЯADC=ЁЯOAD+ЁЯADC=ЁЯARC=45ЁуЃЌЁрЁЯAQD=45ЁуЃЎ
ЁпAC2=12+22=5ЃЌAD2=(5+1)2+32=45ЃЌDC2=52+(2+3)2=50ЃЌЁрAC2+AD2=5+45=50= DC2ЃЌЁрЁЯCAD=90ЁуЃЌЁрЁЯQAD=90ЁуЃЎ
ЁпЁЯAQD=45ЁуЃЌЁрЁїAQDЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрAQ=ADЃЎ
ЁпЁЯQAD=90ЁуЃЌЁрЁЯNAQ+ЁЯDAM=90ЁуЃЎ
ЁпЁЯNAQ+ЁЯAQN=90ЁуЃЌЁрЁЯAQN=ЁЯMADЃЎдкЁїQANКЭЁїADMжаЃЌЁпЁЯAQN=ЁЯMADЃЌЁЯQNA=ЁЯAMD=90ЁуЃЌAQ=ADЃЌЁрЁїQANЁеЁїADMЃЌЁрNA=DM=3ЃЌQN=AM=6ЃЌЁрON=4ЃЌЁрNЃЈЃ4ЃЌ0ЃЉЃЎЩшPЃЈxЃЌyЃЉЃЎ
ЁпQPЁЮyжсЃЌЁрPЕуКсзјБъЮЊx=-4ЃЌЁрy=![]() =Ѓ12ЃЌЁрPN=12ЃЌЁрPQ=PN-QN=12Ѓ6=6ЃЎ
=Ѓ12ЃЌЁрPN=12ЃЌЁрPQ=PN-QN=12Ѓ6=6ЃЎ


 ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
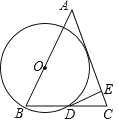
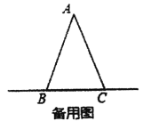
ЁОЬтФПЁПШчЭМЃЌЕу O ЪЧЁїABC ЕФБп AB ЩЯвЛЕуЃЌвд OB ЮЊАыОЖЕФЁбO НЛ BC гкЕу DЃЌЙ§Еу D ЕФЧаЯпНЛ AC гкЕу EЃЌЧв DEЁЭACЃЎ
(1)жЄУїЃКABЃНACЃЛ
(2)Щш ABЃН![]() cmЃЌBCЃН2cmЃЌЕБЕу O дк AB ЩЯвЦЖЏЕНЪЙЁбO гыБп AC ЫљдкжБЯпЯрЧаЪБЃЌ ЧѓЁбO ЕФАыОЖЃЎ
cmЃЌBCЃН2cmЃЌЕБЕу O дк AB ЩЯвЦЖЏЕНЪЙЁбO гыБп AC ЫљдкжБЯпЯрЧаЪБЃЌ ЧѓЁбO ЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
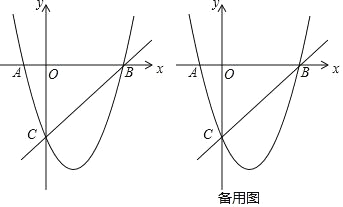
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§ЕФЭМЯѓНЛзјБъжсгк AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌC
ЃЈ0ЃЌЉ4ЃЉШ§ЕуЃЌЕу P ЪЧжБЯп BC ЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉ ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉ ЪЧЗёДцдкЕу PЃЌЪЙЁїPOC ЪЧвд OC ЮЊЕзБпЕФЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГі P ЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉ дкХзЮяЯпЩЯЪЧЗёДцдкЕу DЃЈгыЕу A ВЛжиКЯЃЉЪЙЕУ SЁїDBCЃНSЁїABCЃЌШєДцдкЃЌЧѓГіЕу DЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЫљдкЕФжБЯпЩЯЃЌЕу
ЫљдкЕФжБЯпЩЯЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
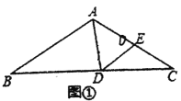
ЃЈ1ЃЉШчЭМЂйЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
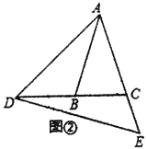
ЃЈ2ЃЉШчЭМЂкЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЩЯ(ВЛгыЕу
ЩЯ(ВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯ)дЫЖЏЪБЃЌЪдЬНОП
жиКЯ)дЫЖЏЪБЃЌЪдЬНОП![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
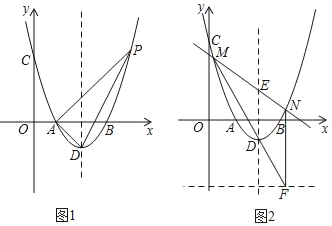
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+cгыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌХзЮяЯпЖЅЕуЮЊDЕуЃЎ
(1)ЧѓДЫХзЮяЯпНтЮіЪНЃЛ
(2)ШчЭМ1ЃЌЕуPЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкЖдГЦжсгвВрЃЌШєЁїADPУцЛ§ЮЊ3ЃЌЧѓЕуPЕФзјБъЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌPAНЛЖдГЦжсгкЕуEЃЌШчЭМ2ЃЌЙ§EЕуЕФШЮвЛЬѕжБЯпгыХзЮяЯпНЛгкMЃЌNСНЕуЃЌжБЯпMDНЛжБЯпyЃНЉ3гкЕуFЃЌСЌНсNFЃЌЧѓжЄЃКNFЁЮyжсЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌдкБп
ЕФжаЕуЃЌдкБп![]() ЩЯШЁЕу
ЩЯШЁЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЎШЦЕу
ЃЎШЦЕу![]() а§зЊ
а§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЈЕу
ЃЈЕу![]() ЁЂ
ЁЂ![]() ЗжБ№гыЕу
ЗжБ№гыЕу![]() ЁЂ
ЁЂ![]() ЖдгІЃЉЃЌЕБ
ЖдгІЃЉЃЌЕБ![]() ЪБЃЌдђ
ЪБЃЌдђ![]() ___________ЃЎ
___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
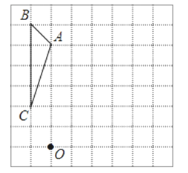
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ЕФе§ЗНаЮЃЌЁїABCЕФЖЅЕуЖМдкИёЕуЩЯЃЌЧыЭъГЩЯТСаШЮЮёЃК
ЃЈ1ЃЉНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ90ЁуКѓЕУЕНЁїA1B1CЃЛ
ЃЈ2ЃЉЧѓЯпЖЮACа§зЊЕНA1CЕФЙ§ГЬжаЃЌЫљЩЈЙ§ЕФЭМаЮЕФУцЛ§ЃЛ
ЃЈ3ЃЉвдЕуOЮЊЮЛЫЦжааФЃЌЮЛЫЦБШЮЊ2ЃЌНЋЁїA1B1CЗХДѓЕУЕНЁїA2B2C2ЃЈдкЭјИёжЎФкЛЭМЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖЅЕуЮЊMЕФХзЮяЯпy=ax2+bxЃЈaЃО0ЃЉЃЌОЙ§ЕуAКЭxжсе§АыжсЩЯЕФЕуBЃЌAO=OB=2ЃЌЁЯAOB=120ЁуЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНгOMЃЌЧѓЁЯAOMЕФДѓаЁЃЛ
ЃЈ3ЃЉШчЙћЕуCдкxжсЩЯЃЌЧвЁїABCгыЁїAOMЯрЫЦЃЌЧѓЕуCЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy1=aЃЈx+2ЃЉ2Љ3гыy2=![]() ЃЈxЉ3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЃЈxЉ3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЂйЮоТлxШЁКЮжЕЃЌy2ЕФжЕзмЪЧе§Ъ§ЃЛ
Ђкa=1ЃЛ
ЂлЕБx=0ЪБЃЌy2Љy1=4
Ђм2AB=3ACЃЎ
Цфжае§ШЗНсТлЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com