
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.

【答案】(1) y=![]() x2﹣
x2﹣![]() x;(2) ∠AOM=150°;(3)点C的坐标为:(4,0)或(8,0).
x;(2) ∠AOM=150°;(3)点C的坐标为:(4,0)或(8,0).
【解析】
试题分析:(1)根据AO=OB=2,∠AOB=120°,求出A点坐标,以及B点坐标,进而利用待定系数法求二次函数解析式;(2)根据(1)中解析式求出M点坐标,再利用锐角三角函数关系求出∠FOM=30°,进而得出答案;(3)分别根据当△ABC1∽△AOM以及当△C2BA∽△AOM时,利用相似三角形的性质求出C点坐标即可.
试题解析:(1)过点A作AE⊥y轴于点E,
∵AO=OB=2,∠AOB=120°,
∴∠AOE=30°,
∴OE=![]() ,AE=1,
,AE=1,
∴A点坐标为:(﹣1,![]() ),B点坐标为:(2,0),
),B点坐标为:(2,0),
将两点代入y=ax2+bx得:
 ,
,
解得: ,
,
∴抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x;
x;

(2)过点M作MF⊥OB于点F,
∵y=![]() x2﹣
x2﹣![]() x=
x=![]() (x2﹣2x)=
(x2﹣2x)=![]() (x2﹣2x+1﹣1)=
(x2﹣2x+1﹣1)=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴M点坐标为:(1,﹣![]() ),
),
∴tan∠FOM=![]() =
=![]() ,
,
∴∠FOM=30°,
∴∠AOM=30°+120°=150°;
(3)当点C在x轴负半轴上时,则∠BAC=150°,而∠ABC=30°,此时∠C=0°,故此种情况不存在;
当点C在x轴正半轴上时,
∵AO=OB=2,∠AOB=120°,
∴∠ABO=∠OAB=30°,
∴AB=2EO=2![]() ,
,
当△ABC1∽△AOM,
∴![]() ,
,
∵MO=![]() =
=![]() ,
,
∴ ,
,
解得:BC1=2,∴OC1=4,
∴C1的坐标为:(4,0);
当△C2BA∽△AOM,
∴![]() ,
,
∴ ,
,
解得:BC2=6,∴OC2=8,
∴C2的坐标为:(8,0).
综上所述,△ABC与△AOM相似时,点C的坐标为:(4,0)或(8,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小丽想用一块面积为400平方厘米的正方形纸片,沿着边的方向裁出一块面积为300平方厘米的长方形纸片,使它的长宽之比为3:2.不知能否裁出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(①)为雅婷左手拿着3张深灰色与2张浅灰色的牌迭在一起的情形.以下是她每次洗牌的三个步骤:
步骤一:用右手拿出迭在最下面的2张牌,如图(②).
步骤二:将右手拿的2张牌依序交错插入左手拿的3张牌之间,如图(③).
步骤三:用左手拿着颜色顺序已改变的5张牌,如图(④).
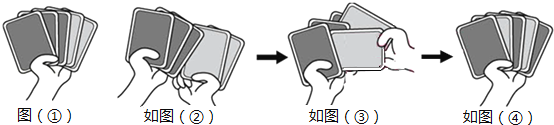
若依上述三个步骤洗牌,从图(①)的情形开始洗牌若干次后,其颜色顺序会再次与图(①)相同,则洗牌次数可能为下列何者?( )
A. 18 B. 20 C. 25 D. 27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com