
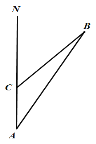
【题目】钓鱼岛自古以来是我国的固有领土,随着我们国家综合国力的强盛,国家对钓鱼岛的巡航已常态化.2017年9月11日,中国海警2401号船在A地测得钓鱼岛B在北偏东30°方向,现该海警船继续从A地出发以30海里/小时的速度向正北方向航行2小时后到达C地.
(1)若∠B=15°,求钓鱼岛B在C地的北偏东多少度?
(2)在(1)的基础上,求海警船与钓鱼岛的距离CB的长.(结果保留根号)
【答案】(1)45°; (2)30![]() +30
+30![]() .
.
【解析】
(1)依据三角形外角性质,即可得到钓鱼岛B在C地的北偏东45度方向上;
(2)过B作BD⊥AC于D,设CD=BD=x,则AD=x+2×30=x+60,运用解直角三角形即可得到海警船与钓鱼岛的距离CB的长为(30![]() 30
30![]() )海里.
)海里.
(1)∵∠B=15°,∠BAC=30°,∴∠BCN=∠B+∠A=45°,即钓鱼岛B在C地的北偏东45度方向上;
(2)如图所示,过B作BD⊥AC于D,则∠CBD=45°,∴CD=BD,设CD=BD=x,则AD=x+2×30=x+60.在Rt△ABD中,tanA![]() ,即
,即![]() ,解得:x=30
,解得:x=30![]() 30,即CD=30
30,即CD=30![]() 30,∴Rt△BCD中,BC
30,∴Rt△BCD中,BC![]() CD=30
CD=30![]() 30
30![]()
答:海警船与钓鱼岛的距离CB的长为(30![]() 30
30![]() )海里.
)海里.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为格点,以格点为顶点的三角形叫做格点三角形,根据图形,回答下列问题.
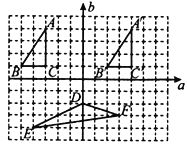
(1)图中格点三角形![]() 是由格点三角形
是由格点三角形![]() 通过怎样的变换得到的?
通过怎样的变换得到的?
(2)如果以直线![]() 为坐标轴建立平面直角坐标系后,点
为坐标轴建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,请写出格点三角形
,请写出格点三角形![]() 各顶点的坐标,并求出三角形
各顶点的坐标,并求出三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于 x 的一元二次方程 a![]() +bx+c=0(a≠0)有两个实数根,且其中一个根比另一个根大 1,那么称这样的方程为“邻根方程”.例如,一元二次方程
+bx+c=0(a≠0)有两个实数根,且其中一个根比另一个根大 1,那么称这样的方程为“邻根方程”.例如,一元二次方程![]() +x=0 的两个根是
+x=0 的两个根是 ![]() =0,
=0,![]() =﹣1,则方程
=﹣1,则方程 ![]() +x=0 是“邻根方程”.
+x=0 是“邻根方程”.
(1)通过计算,判断下列方程是否是“邻根方程”:
①![]() ﹣x﹣6=0;
﹣x﹣6=0;
②2![]() ﹣2
﹣2![]() x+1=0.
x+1=0.
(2)已知关于 x 的方程![]() ﹣(m﹣1)x﹣m=0(m 是常数)是“邻根方程”,求 m 的值;
﹣(m﹣1)x﹣m=0(m 是常数)是“邻根方程”,求 m 的值;
(3)若关于 x 的方程 a![]() +bx+1=0(a、b 是常数,a>0)是“邻根方程”,令 t=8a-
+bx+1=0(a、b 是常数,a>0)是“邻根方程”,令 t=8a-![]() ,试求 t 的最大值.
,试求 t 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
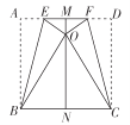
【题目】寒假丽丽用一块边长为10的正方形彩纸为她的人偶玩具做了一件披风,如图所示,先将正方形纸片![]() 对折,展平后得到中线
对折,展平后得到中线![]() ,再分别沿折痕
,再分别沿折痕![]() ,
,![]() 将点
将点![]() ,点
,点![]() 都折到
都折到![]() 上点
上点![]() 处,此时领口
处,此时领口![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克 40 元,规定每千克售价不低于成本,且不高于 80 元,经市场调查,每天的销售量 y( 千克)与每千克售价x(元)满足一次函数关系,部分数据如表:

(1)求 y 与 x 之间的函数表达式;
(2)设商品每天的总利润为 W(元),求 W 与 x 之间的函数表达式(利润=收入﹣成本);
(3)指出售价为多少元时获得利润最大?并试说明(2)中总利润W随售价x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com