
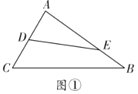
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
【答案】![]() 4
4
【解析】
如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可.
解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.
∵AM⊥CD,
∴∠QMP=∠MPO=∠OQM=90°,
∴四边形OQMP是矩形,
∴QM=OP,
∵OC=OD=10,∠COD=60°,
∴△COD是等边三角形,
∵OP⊥CD,
∴∠COP=![]() ∠COD=30°,
∠COD=30°,
∴QM=OP=OCcos30°=5![]() (分米),
(分米),
∵∠AOC=∠QOP=90°,
∴∠AOQ=∠COP=30°,
∴AQ=![]() OA=5(分米),
OA=5(分米),
∴AM=AQ+MQ=5+5![]() .
.
∵OB∥CD,
∴∠BOD=∠ODC=60°
在Rt△OFK中,KO=OFcos60°=2(分米),FK=OFsin60°=2![]() (分米),
(分米),
在Rt△PKE中,EK=![]() =2
=2![]() (分米),
(分米),
∴BE=1022![]() =(82
=(82![]() )(分米),
)(分米),
在Rt△OFJ中,OJ=OFcos60°=2(分米),FJ=2![]() (分米),
(分米),
在Rt△FJE′中,E′J=![]() =2
=2![]() ,
,
∴B′E′=10(2![]() 2)=122
2)=122![]() ,
,
∴B′E′BE=4.
故答案为5+5![]() ,4.
,4.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,一条直线
,一条直线![]() 与边
与边![]() 相交于点
相交于点![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
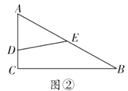
(1)如图①,若![]() 将
将![]() 分成周长相等的两部分,求
分成周长相等的两部分,求![]() 的值;(用
的值;(用![]() 、
、![]() 、
、![]() 表示)
表示)
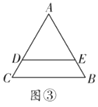
(2)如图②,若![]() ,
,![]() ,
,![]() ,
,![]() 将
将![]() 分成周长、面积相等的两部分,求
分成周长、面积相等的两部分,求![]() 的值;
的值;
(3)如图③,若![]() 将
将![]() 分成周长、面积相等的两部分,且
分成周长、面积相等的两部分,且![]() ,则
,则![]() 、
、![]() 、
、![]() 满足什么关系?
满足什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,且
,且![]() 点的坐标为
点的坐标为![]() .
.
(1)求该抛物线的解析式.
(2)如图1,若点![]() 是线段
是线段![]() 上的一动点,过点
上的一动点,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
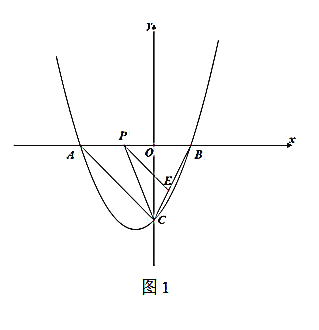
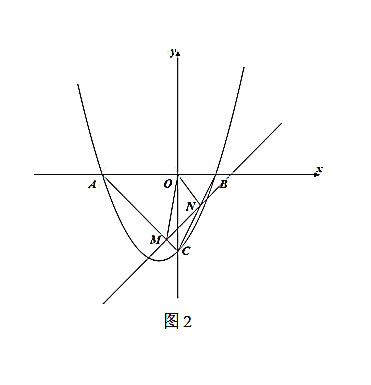
(3)如图2,若直线![]() 与线段
与线段![]() 交于点
交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,是否存在
,是否存在![]() ,
,![]() ,使得
,使得![]() 为直角三角形,若存在,请求出
为直角三角形,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
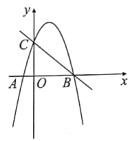
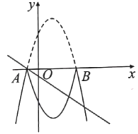
(1)求抛物线的表达式;
(2)过点![]() 的直线
的直线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 平分
平分![]() 的面积时,求点
的面积时,求点![]() 的坐标;
的坐标;
(3)如图所示,把抛物线位于![]() 轴上方的图象沿
轴上方的图象沿![]() 轴翻折,当直线
轴翻折,当直线![]() 与翻折后的整个图象只有三个交点时,求
与翻折后的整个图象只有三个交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为迎接县中学生篮球比赛,计划购买A、B两种篮球共20个供学生训练使用.若购买A种篮球6个,则购买两种篮球共需费用720元;若购买A种篮球12个,则购实两种篮球共需费用840元.
(1)A、B两种篮球共需单价各多少元?
(2)设购买A种篮球x个且A种篮球不少于8个,所需费用为y元,试确定y与x的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com