
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,且
,且![]() 点的坐标为
点的坐标为![]() .
.
(1)求该抛物线的解析式.
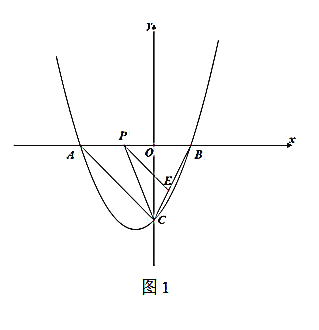
(2)如图1,若点![]() 是线段
是线段![]() 上的一动点,过点
上的一动点,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
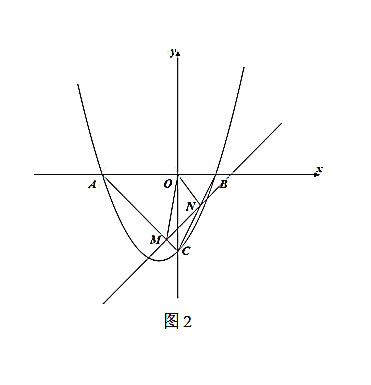
(3)如图2,若直线![]() 与线段
与线段![]() 交于点
交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,是否存在
,是否存在![]() ,
,![]() ,使得
,使得![]() 为直角三角形,若存在,请求出
为直角三角形,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某市某中学积极响应创建全国文明城市活动,举办了以“校园文明”为主题的手抄报比赛.所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如右两幅统计图.请你根据图中所给信息解答意)
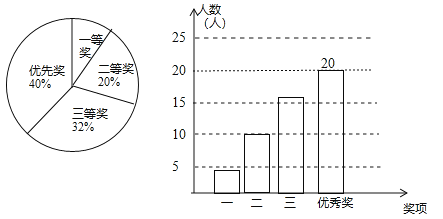
(1)等奖所占的百分比是________;三等奖的人数是________人;
(2)据统计,在获得一等奖的学生中,男生与女生的人数比为![]() ,学校计划选派1名男生和1名女生参加市手抄报比赛,请求出所选2位同学恰是1名男生和1名女生的概率;
,学校计划选派1名男生和1名女生参加市手抄报比赛,请求出所选2位同学恰是1名男生和1名女生的概率;
(3)学校计划从获得二等奖的同学中选取一部分人进行集训使其提升为一等奖,要使获得一等奖的人数不少于二等奖人数的2倍,那么至少选取多少人进行集训?
查看答案和解析>>
科目:初中数学 来源: 题型:
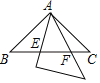
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
A.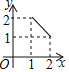 B.
B.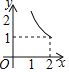 C.
C.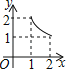 D.
D.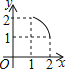
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为□ABCD中一点,EA=ED,∠AED=90,点F,G分别为AB,BC上的点,连接DF,AG,AD=AG=DF,且AG⊥DF于点H,连接EG,DG,延长AB,DG相交于点P.
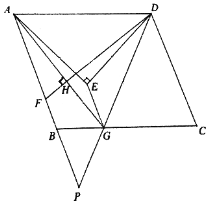
(1)若AH=6,FH=2,求AE的长;
(2)求证:∠P=45;
(3)若DG=2PG,求证:∠AGE=∠EDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
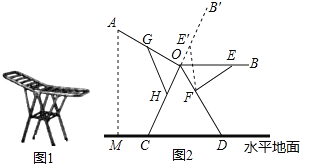
查看答案和解析>>
科目:初中数学 来源: 题型:
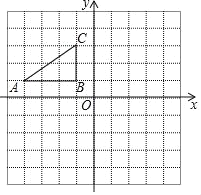
【题目】如图,在平面直角坐标系中,小正方形格子的边长为1,Rt△ABC三个顶点都在格点上,请解答下列问题:
(1)写出A,C两点的坐标;
(2)画出△ABC关于原点O的中心对称图形△A1B1C1;
(3)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2,并直接写出点C旋转至C2经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
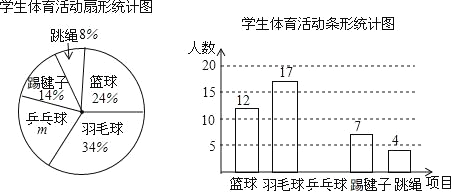
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x的图象与反比例函数y=![]() 的图象交于点(a,2).
的图象交于点(a,2).
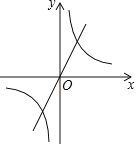
(1)求a和k的值.
(2)若点P(m,n)在反比例函数图象上,且点P到y轴的距离小于1,请根据图象直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com