
����Ŀ����ϰ���У���ʦ��������x�ĺ���y=2kx2-��4k+1��x-k+1��k��ʵ��������ʦ�������˼��������̽�����ֵ���ú����йصĽ��ۣ����ʣ�д���ڰ��ϣ�ѧ��˼���ڰ��ϳ�����һЩ���ۣ���ʦ��Ϊ�һԱ���ֲ���һЩ���ۣ�������ѡ������������
�����ں�������ͼ����1��0���㣻
�����ں������ú����ĺ���ֵyʼ����x���������С��
������ͼ���п��ܾ����������ޣ�
�������������ֵ�������ֵ��Ϊ����������������Сֵ������Сֵ��Ϊ������
������ȷ�Ľ����� ��
���𰸡��٢ڢ�
��������
�ٽ���1��0������뺯�������k��ֵ���������жϣ�
�����ȿ��ǣ�����Ϊһ�κ�����������Ӷ����ж�Ϊ�٣�
�۸��ݢڼ��������жϣ�
�ܵ�k=0ʱ������Ϊһ�κ����������֮����Сֵ����k��0ʱ������Ϊ�����ߣ������������������ʽ�����������жϣ�
������1��0������ɵã�2k-��4k+1��-k+1=0����ã�k=0����ѡ����ȷ��
����k=0ʱ��y=-x+1���ú����ĺ���ֵyʼ����x���������С����ѡ����ȷ��
��y=-x+1������3�����ޣ���ѡ�����
����k=0ʱ�������������Сֵ��k��0ʱ��y��=-![]() ����k��0ʱ������Сֵ����СֵΪ������k��0ʱ�������ֵ�����ֵΪ������ѡ����ȷ��
����k��0ʱ������Сֵ����СֵΪ������k��0ʱ�������ֵ�����ֵΪ������ѡ����ȷ��
��ȷ�����٢ڢ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
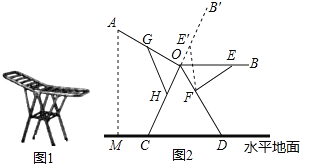
����Ŀ��ͼ1��һ���۵�ʽ���¼ܣ�����ʱ�������¼��������±��ſ���ʾ��ͼ��ͼ2��ʾ����֧��OC��OD��10���ף�չ���ǡ�COD��60�㣬���±�OA��OB��10���ף����±�֧��HG��FE��6���ף���HO��FO��4���ף�����AOC��90��ʱ����A�����ľ���AMΪ_______���ף���OB��ˮƽ״̬��ת��OB�䣨��CO�ӳ����ϣ�ʱ����E�Ƶ�F��֮��ת��OB���ϵĵ�E�䴦����B��E�䩁BEΪ_________���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�����õ�涨���£����ÿ��һ���µ��õ���������![]() �ȣ���ô�����ֻ��Ҫ��10Ԫ��ѣ�������
�ȣ���ô�����ֻ��Ҫ��10Ԫ��ѣ�������![]() �ȣ�������³���Ҫ��10Ԫ����⣬�����IJ��ֻ�Ҫ��
�ȣ�������³���Ҫ��10Ԫ����⣬�����IJ��ֻ�Ҫ��![]() Ԫ���ѣ��±���ij��5�·ݺ�6�·ݵ��õ�ͽ����������
Ԫ���ѣ��±���ij��5�·ݺ�6�·ݵ��õ�ͽ����������![]() ��ֵ.
��ֵ.
�·� | �õ������ȣ� | �����������Ԫ�� |
5 | 80 | 25 |
6 | 45 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD������A��1��3����B��1��1����C��3��1�����涨����������ABCD����x�ᷭ�ۣ�������ƽ��1����λ��Ϊһ�α任�������������������2014�α任��������ABCD�ĶԽ��߽���M�������Ϊ�� ��
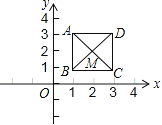
A.��-2012��2��B.��-2012��-2��C.��-2013��-2��D.��-2013��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
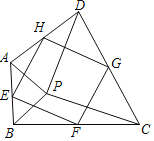
��1����ͼ����P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��2�����ı䣨1���е�������ʹ��APB����CPD��90���������������䣬ֱ��д���е��ı���EFGH����״������֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ�ۺ�ʵ����У�С���ƻ��������Ŵ�¥�ĸ߶ȣ��ڵ�B�����¥��A������Ϊ22�����������ų�¥ǰ��21����C�����ٵ���3�ߵ�¥̨D��������ô�ʱ¥��A������Ϊ45����
��1������Ŵ�¥�ĸ߶ȣ�
��2��ÿ���ش���գ����Ŵ�¥��������Ҫ��A��B֮���������ӣ����������Ϲ�һЩ���죬�������A��B֮�����Ҳ���ij��ȣ�������������������ο����ݣ�sin22���![]() ��cos22���
��cos22���![]() ��tan22���
��tan22���![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һԪ���η���M��ax2+bx+c=0��N��cx2+bx+a=0������ac��0��a��c�������ĸ������У���ȷ�ĸ����У�������
���������M��������ȵ�ʵ��������ô����NҲ��������ȵ�ʵ������
�����ac��0������M��N������������ȵ�ʵ������
�����2�Ƿ���M��һ��������ô![]() �Ƿ���N��һ������
�Ƿ���N��һ������
���������M�ͷ���N��һ����ͬ�ĸ�����ô���������x=1��
A.4��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA��2��OC��3��
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA��2��OC��3��
��1���������ߵĽ���ʽ��
��2����D��2��2������������һ�㣬��ô�������ߵĶԳ����ϣ��Ƿ����һ��P��ʹ����BDP���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������AD���ӳ�������������һ��Q��Q����A�غϣ���QN��x�ᣬ����ΪN�������߽��ڵ�M��ʹ��QM��3MN�������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com