
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式.
上的“闭函数”,求此一次函数的解析式.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】下列式子正确的是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a﹣b)2=a2+2ab+b2
D.(a﹣b)2=a2﹣ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式x3﹣xy2+x2y+x4﹣3按x的降幂排列,正确的是( )
A.x4+x3+x2y﹣3﹣xy2
B.﹣xy2+x2y+x4+x3﹣3
C.﹣3﹣xy2+x2y+x3+x4
D.x4+x3+x2y﹣xy2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( )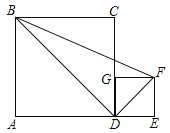
A.4.5
B.3
C.4
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
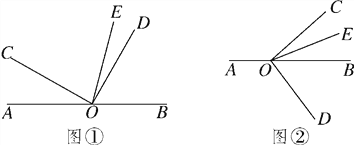
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
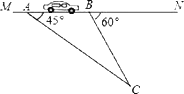
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作,现要在流水生产线上设置一个零件供应站P,使五人到供应站P的距离总和最小,这个供应站设置的位置是( )
![]()
A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com