
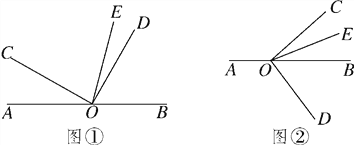
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
【答案】(1)15°;(2)![]() ;(3)①∠AOC=2∠DOE;②4∠DOE-5∠AOF=180°.
;(3)①∠AOC=2∠DOE;②4∠DOE-5∠AOF=180°.
【解析】试题分析:(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
②设∠DOE=x,∠AOF=y,根据已知和:∠AOC-4∠AOF=2∠BOE+∠AOF,得出4x-5y=180,从而得出结论.
解:(1)由已知得∠BOC=180°-∠AOC=150°,又∠COD是直角,OE平分∠BOC,∴∠DOE=∠COD-![]() ∠BOC=90°-
∠BOC=90°-![]() ×150°=15°.
×150°=15°.
(2)∠DOE=![]() a. 解析:由(1)知∠DOE=∠COD-
a. 解析:由(1)知∠DOE=∠COD-![]() ∠BOC=90°,∴∠DOE=90°-
∠BOC=90°,∴∠DOE=90°-![]() (180°-∠AOC)=
(180°-∠AOC)=![]() ∠AOC=
∠AOC=![]() α.
α.
(3)①∠AOC=2∠DOE.理由如下:
∵∠COD是直角,OE平分∠BOC,
∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),∴∠AOC=2∠DOE.
②4∠DOE-5∠AOF=180°.
理由如下:设∠DOE=x,∠AOF=y,
∴∠AOC-4∠AOF=2∠DOE-4∠AOF=2x-4y,2∠BOE+∠AOF=2(90°-x)+y=180°-2x+y,
∴2x-4y=180°-2x+y,即4x-5y=180°,
∴4∠DOE-5∠AOF=180°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式.
上的“闭函数”,求此一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() , 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .
, 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .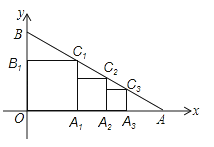
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .四个结论中正确结论的概率是( )
.四个结论中正确结论的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com