
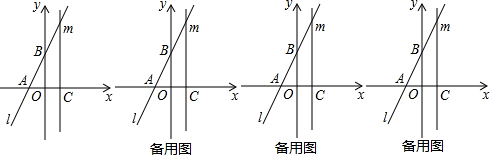
���� ��1���ֱ���x=0��y=0�������A��B�����ꣻ
��2����x�����ҵ�A����x=1�ĶԳƵ�ΪA�䣬����A��B��m�ڵ�P����PA+PB=PA��+PB��С�����ݹ��ɶ��������A��B��������������M�����ꣻ
��3�����MΪ��1��y������MA=MB��MB=AB��MA=AB��������õ�������y�ķ��̣������M�����ꣻ
��4������ͼ�Σ����û��ഹֱ��ֱ��֮��Ĺ�ϵ�����ô���ϵ�������ֱ��AN�Ľ���ʽ�������x=1ʱ�������꣬�������N������꣮
��� �⣺��1����y=2x+2��
����y=0�ɵ�x=-1����x=0�ɵ�y=2��
��A����-1��0����B����0��2����
��2����ֱ��m����C��1��0����
��ֱ��m�ķ���Ϊx=1��
��A�����ֱ��x=1�ĶԳƵ�ΪA�䣨3��0����
��ͼ1������A��B��m�ڵ�P����PA+PB=PA��+PB=A��B��С��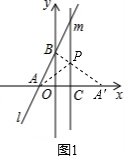
��Rt��OBA���У�OB=2��OA��=3���ɹ��ɶ��������A��B=$\sqrt{13}$��
��ֱ��m��x�ᴹֱ��
��ֱ��m��y�ᣬ
���A��PC�ס�A��BO��
��$\frac{PC}{BO}$=$\frac{A��C}{A��O}$����$\frac{PC}{2}$=$\frac{2}{3}$��
���PC=$\frac{4}{3}$��
��P��������1��$\frac{4}{3}$����
�൱P��Ϊ��1��$\frac{4}{3}$��ʱ��PA+PB������СֵΪ$\sqrt{13}$��
��3����M��������1��y����
���ɹ��ɶ�����֪AB2=5��AM2=��1+1��2+y2=4+y2��BM=12+��y-2��2=1+��y-2��2��
�ߡ�MABΪ���������Σ�
���MA=MB��MB=AB��MA=AB���������
��MA=MBʱ����AM2=BM2������4+y2=1+��y-2��2�����y=$\frac{1}{4}$����ʱM������Ϊ��1��$\frac{1}{4}$����
��MB=ABʱ����MB2=AB2������5=1+��y-2��2�����y=0��y=4����ȥ������ʱMΪ��1��0����
��MA=ABʱ����MA2=AB2������5=4+y2�����y=-1��y=1����ʱMΪ��1��-1����1��1����
���Ͽ�֪M�������Ϊ��1��$\frac{1}{4}$����1��0����1��-1����1��1����
��4��N���λ����ͼ2��ʾ��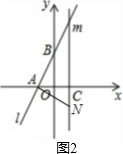
�ߡ�BAN���ԡ�BANΪֱ�ǵ�ֱ�������Σ�
����ֱ��AN�Ľ���ʽΪy=-$\frac{1}{2}$x+b����$\frac{1}{2}$+b=0��
���b=-$\frac{1}{2}$��
��ֱ��AN�Ľ���ʽΪy=-$\frac{1}{2}$x-$\frac{1}{2}$��
��x=1ʱ��y=-$\frac{1}{2}$-$\frac{1}{2}$=-1��
��N��������1��-1����
���� ������Ҫ������ֱ����������Ľ������ԳƵ����ʡ����������ε����ʡ����������ε��ж������ʼ����ɶ�����Ӧ�ã��ڣ�2����ȷ����P���λ���ǽ���Ĺؼ����ڣ�3�������M�������ֱ��ʾ��AB��MA��MB�ij��ȣ���������������ǹؼ����ڣ�4����ע�����û��ഹֱ��ֱ��֮��Ĺ�ϵ������ϵ��������N�����֪꣮ʶ��϶࣬�ѶȽϴ�ע�����˼��ͷ���˼���Ӧ�ã�


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
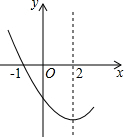 ��ͼ��������y=ax2+bx+c��a��0��ͼ���һ���֣���y��0ʱ���Ա���x�ķ�Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0��ͼ���һ���֣���y��0ʱ���Ա���x�ķ�Χ�ǣ�������| A�� | x��-1��x��2 | B�� | x��-1��x��5 | C�� | -1��x��5 | D�� | -1��x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڳ�����ABCD��AB=6�ף�BC=8�ף�����P��2��/����ٶȴӵ�A��������AC���C�ƶ���ͬʱ����Q��1��/����ٶȴӵ�C��������CB���B�ƶ�����F��Q�����ƶ�t�루0��t��5����
��ͼ���ڳ�����ABCD��AB=6�ף�BC=8�ף�����P��2��/����ٶȴӵ�A��������AC���C�ƶ���ͬʱ����Q��1��/����ٶȴӵ�C��������CB���B�ƶ�����F��Q�����ƶ�t�루0��t��5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
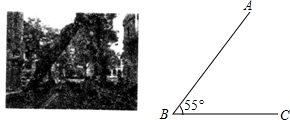 ��ͼ����б�Ĵ��������ļнǡ�ABCΪ55�㣬��Ϊ3.5�Ĵ�ͳ�����������һ������Ҫ������ĸ���B������ײ��ܰ�ȫͨ�����������ȷ��0.1�ף�
��ͼ����б�Ĵ��������ļнǡ�ABCΪ55�㣬��Ϊ3.5�Ĵ�ͳ�����������һ������Ҫ������ĸ���B������ײ��ܰ�ȫͨ�����������ȷ��0.1�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | �� | -1 | 0 | 1 | �� |
| y | �� | 0 | 1 | m | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com