
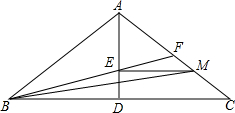
 如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S.
如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S.分析 (1)先证明△AEM∽△ADC,进而得到AE:AD=EM:DC=AM:AC=2:3,设AE=2a,则AD=3a,EM=2b,则DC=3b,即可求$\frac{{{S_{△ABE}}}}{{{S_{△BME}}}}$的值;
(2)根据△AEM∽△ADC得到$\frac{AE}{AD}=\frac{EM}{DC}=\frac{AM}{AC}=\frac{1-m}{1}$,即AE=3-3m,DE=3m,EM=4-4m,据此写出S关于m的二次函数,结合二次函数的性质求出最值;
(3)根据三角形的面积与边长之间的关系求出k和m的数量关系.
解答 解:(1)∵ME⊥AD,AD⊥BC,
∴△AEM∽△ADC,
∴$\frac{AE}{AD}=\frac{EM}{DC}=\frac{AM}{AC}=\frac{1-m}{1}=\frac{2}{3}$,
设AE=2a,则AD=3a.EM=2b,则DC=3b,
∴$\frac{{{S_{△ABE}}}}{{{S_{△BME}}}}=\frac{{2a×3b×\frac{1}{2}}}{{2b×a×\frac{1}{2}}}=3$;
(2)∵△AEM∽△ADC,
∴$\frac{AE}{AD}=\frac{EM}{DC}=\frac{AM}{AC}=\frac{1-m}{1}$,
∴AE=3-3m,DE=3m,EM=4-4m
∴S=$\frac{1}{2}×(4-4m)×3m$,
当m=$\frac{1}{2}$时,S最大=$\frac{3}{2}$;
(3)$\frac{AF}{FM}=\frac{{{S_{△AEF}}}}{{{S_{△EFM}}}}=\frac{{{S_{△ABF}}}}{{{S_{△BMF}}}}=k$$\frac{{{S_{△ABE}}}}{{{S_{△BME}}}}=\frac{{{S_{△ABF}}-{S_{△AEF}}}}{{{S_{△BFM}}-{S_{△EFM}}}}=k$$\frac{{{S_{△ABE}}}}{{{S_{△BME}}}}=\frac{AE×BD}{EM×ED}=\frac{AE×CD}{EM×ED}=\frac{AD×EM}{EM×ED}=\frac{AD}{ED}=\frac{1}{m}$,
即k=$\frac{1}{m}$.
点评 本题主要考查了相似三角形的判定与性质以及二次函数的最值的知识,解答本题的关键是证明△AEM∽△ADC,解答此题还要掌握三角形面积的计算,此题难度一般.


科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:单选题
如图所示,已知直线AB∥CD,用含∠1、∠ 2、∠ 3的式子表示∠ 4,则 ∠ 4 的值为( )
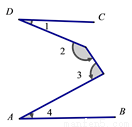
A. ∠1+∠ 2-∠ 3 B. ∠1+∠ 3-∠ 2
C. 180°+∠ 3-∠1-∠ 2 D. ∠ 2+∠ 3-∠1-180°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
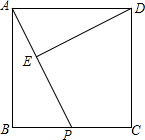 如图,正方形ABCD中,AB=4$\sqrt{5}$,P是BC的中点,DE⊥AP,垂足为点E.
如图,正方形ABCD中,AB=4$\sqrt{5}$,P是BC的中点,DE⊥AP,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
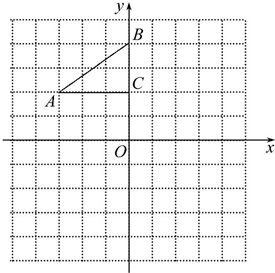 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
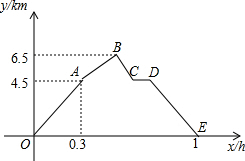 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.如果小明两次经过途中某一地点的时间间隔为0.12h,那么该地点离甲地5.7km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
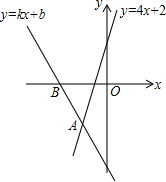 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 1 | 2 | 9 | 10 | 25 | … |
| 4 | 3 | 8 | 11 | 24 | … |
| 5 | 6 | 7 | 12 | 23 | … |
| 16 | 15 | 14 | 13 | 22 | … |
| 17 | 18 | 19 | 20 | 21 | … |
| … | … | … | … | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com