
����Ŀ����ƽ��ֱ������ϵ�У�������y=x2+��k��1��x��k��ֱ��y=kx+1����A��B���㣬��A�ڵ�B����࣮


��1����ͼ1����k=1ʱ��ֱ��д��A��B��������ꣻ
��2���ڣ�1���������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
��3����ͼ2��������y=x2+��k��1��x��k��k��0����x�ύ�ڵ�C��D���㣨��C�ڵ�D����ࣩ����ֱ��y=kx+1���Ƿ����Ψһһ��Q��ʹ����OQC=90���������ڣ��������ʱk��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��A(-1,0) ��B(2,3)
��2����ABP������s=![]() ; P��
; P��![]() ,-
,-![]() ��
��
��3�����ڣ�k=![]()
��������
���⣨1�� ��k=1ʱ�������߽���ʽΪy=x2��1��ֱ�߽���ʽΪy=x+1��Ȼ��ⷽ����![]() ���ɣ�
���ɣ�
��2�� ��P��x��x2��1��������P��PF��y�ᣬ��ֱ��AB�ڵ�F����F��x��x+1������������S��ABP=S��PFA+S��PFB��
���ú�x�Ĵ���ʽ��ʾΪS��ABP=��x2+x+2���䷽���ù�ʽȷ���������꼴�ɣ���3�� ��ֱ��AB��y=kx+1��x�ᡢy��ֱ��ڵ�E��F����k�ֱ��ʾ��E�����꣬��F�����꣬�Լ���C�����꣬Ȼ����Rt��EOF�У��ɹ��ɶ�����ʾ��EF�ij����������Ψһһ��Q��ʹ����OQC=90��������OCΪֱ����Բ��ֱ��AB�����ڵ�Q�����NΪOC�е㣬����NQ����������֤����EQN�ס�EOF��Ȼ��������ʶ�Ӧ�߳ɱ������ɵù���k�ķ��̣��ⷽ�̼���.
����������⣺��1����k=1ʱ�������߽���ʽΪy=x2��1��ֱ�߽���ʽΪy=x+1��
������������ʽ���ã�x2��1=x+1��
��ã�x=��1��x=2��
��x=��1ʱ��y=x+1=0����x=2ʱ��y=x+1=3��
��A����1��0����B��2��3���� 4��
��2����P��x��x2��1����
���ͼ2��ʾ������P��PF��y�ᣬ��ֱ��AB�ڵ�F����F��x��x+1����
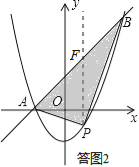
��PF=yF��yP=��x+1������x2��1��=��x2+x+2��
S��ABP=S��PFA+S��PFB=PF��xF��xA��+PF��xB��xF��=PF��xB��xA��=PF
��S��ABP=����x2+x+2��=����x��![]() ��2+
��2+![]()
��x=![]() ʱ��yP=x2��1=��
ʱ��yP=x2��1=��![]() ��
��
���ABP������ֵΪ![]() ����ʱ��P����Ϊ��
����ʱ��P����Ϊ��![]() ����
����![]() ���� 8��
���� 8��
��3����ֱ��AB��y=kx+1��x�ᡢy��ֱ��ڵ�E��F��
��E����![]() ��0����F��0��1����OE=
��0����F��0��1����OE=![]() ��OF=1��
��OF=1��
��Rt��EOF�У��ɹ��ɶ����ã�EF=![]() =
=![]() ��
��
��y=x2+��k��1��x��k=0������x+k����x��1��=0����ã�x=��k��x=1��
��C����k��0����OC=k��
�������Ψһһ��Q��ʹ����OQC=90�������ͼ3��ʾ��
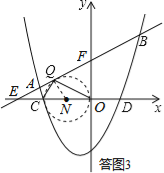
����OCΪֱ����Բ��ֱ��AB�����ڵ�Q������Բ�ܽǶ�������ʱ��OQC=90����
���NΪOC�е㣬����NQ����NQ��EF��NQ=CN=ON=![]() ��
��
��EN=OE��ON=![]() ��
��![]() ��
��
�ߡ�NEQ=��FEO����EQN=��EOF=90����
���EQN�ס�EOF��
��![]() ������
������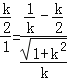 ��
��
��ã�k=��![]() ��
��
��k��0��
��k=![]() ��
��
������Ψһһ��Q��ʹ����OQC=90������ʱk=![]() �� 12��
�� 12��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ�μ��У�ͬѧ�ǻ����μ�����������С����ȫУ�����ȡ��һ����ͬѧ�͡�����ϲ����������Ŀ��������һ�ε��飨ÿλͬѧ��ѡ��ֻѡһ�����������ͨ���ռ������ݻ��Ƶ�������������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
��1��С��һ����ȡ���� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3�������������ֶ�Ӧ������Բ�ĽǵĶ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪����y��![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�B����C���A����y��Գƣ�
x+2��x�ύ�ڵ�A����y�ύ�ڵ�B����C���A����y��Գƣ�

��1����ֱ��BC�ĺ�������ʽ��
��2�����M��x���ϵ�һ�����㣬����M��y��ƽ���ߣ���ֱ��AB�ڵ�P����ֱ��BC�ڵ�Q��
������PQB�����Ϊ![]() �����M�����꣺
�����M�����꣺
���ڢٵ������£���ֱ��PQ����һ��R��ʹ����MOR�ա�MOQ��ֱ��д����R�����ꣻ
��3������BM����ͼ2������BMP����BAC��ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ʵ������Ҫ��һ����ͼ1��ʾ����������������Ŀ���AB�ǹDZ���OA��![]() �������ſ��ĽǶ�Ϊ120����С����Ҫ����ͼ2��ʾ�ľ��β����ϼ��������������治��ƴ������֪���β��ϳ�Ϊ24
�������ſ��ĽǶ�Ϊ120����С����Ҫ����ͼ2��ʾ�ľ��β����ϼ��������������治��ƴ������֪���β��ϳ�Ϊ24![]() cm����Ϊ21cm��С�վ�����ͼ���������ھ��β����ϲü��������������������Ʋü���ճ��ʱ���������ʱ����Ŀ���ABΪ�� ��
cm����Ϊ21cm��С�վ�����ͼ���������ھ��β����ϲü��������������������Ʋü���ճ��ʱ���������ʱ����Ŀ���ABΪ�� ��

A�� 21cm B��20 cm C�� 19cm D�� 18cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC��ƽ��ֱ������ϵ��(0Ϊ����ԭ��)����A��x���ϣ���C��y���ϣ���B������ֱ�Ϊ(��2��2![]() )����E��BC���е㣬��H��OA�ϣ���AH��
)����E��BC���е㣬��H��OA�ϣ���AH��![]() ������H��ƽ����y���HG��EB���ڵ�G���ֽ��������۵���ʹ픵�C����HG�ϵ�D�㴦���ۺ�ΪEF����FΪ�ۺ���y��Ľ���.
������H��ƽ����y���HG��EB���ڵ�G���ֽ��������۵���ʹ픵�C����HG�ϵ�D�㴦���ۺ�ΪEF����FΪ�ۺ���y��Ľ���.
(1)���D�����ꣻ
(2)���ۺ�EF����ֱ�ߵĺ�������ʽ��
(3)����P��ֱ��AB�ϣ�����PFDΪ����������ʱ���������������ĵ�P�м���?�������P�����꣬��д��������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ij��ͯװ��ÿ���ۼ�60Ԫ��ÿ���ڿ���300����Ϊ�˴���������������������ۣ��г����鷴ӳ��ÿ����1Ԫ��ÿ���ڿɶ���30������֪�ÿ�ͯװÿ���ɱ���40Ԫ����ÿ�ͯװÿ���ۼ�xԪ��ÿ���ڵ�������Ϊy����
��1����y��x֮��ĺ�����ϵʽ��
��2����ÿ���ۼ۶�Ϊ����Ԫʱ��ÿ���ڵ����������������������Ԫ��
��3����������ÿ������Ҫ��ò�����6480Ԫ������ÿ��������Ҫ���۸ÿ�ͯװ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƽ��������࣬�ƶ���ɫ��չ��ij���������ס��������ͺŵĻ��������������������࣬���ͻ����˱����ͻ�����ÿСʱ���20kg�����ͻ����˷���800kg�������õ�ʱ�������ͻ����˷���600kg�������õ�ʱ����ȡ�
��1�����ֻ�����ÿСʱ�ֱ�������������
��2���������ֻ����˹�ͬ����700kg����������2Сʱ����ͻ����������ά���˳�������ͻ������˳������ͻ����˻��蹤���ʱ�������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ������Ա��һ���ľߵ�����꼶��ͬѧ���������ľ߰����ľߵ�涨һ�ι���400�����ϣ�������8���Ż�.�������꼶ѧ��ÿ�˹���һ������������8���Żݣ��踶��1936Ԫ��������88�����Ϳ�����8���Żݣ�ͬ��ֻ�踶��1936Ԫ.���ʸ�ѧУ���꼶ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������A��
������A��![]() ��0����B��
��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE����AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com