
【题目】完成下面的证明。
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E。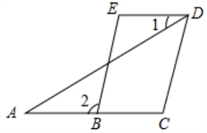
证明:∵BE∥CD (已知 )
∴∠2=∠C ( )
又 ∵∠A=∠1 (已知 )
∴ AC∥DE ( )
∴ ∠2=∠E( )
∴∠C=∠E ( )
【答案】证明:∵BE∥CD (已知 )
∴∠2=∠C ( 两直线平行,同位角相等 )
又 ∵∠A=∠1 (已知 )
∴ AC∥DE ( 内错角相等,两直线平行 )
∴ ∠2=∠E( 两直线平行,内错角相等 )
∴∠C=∠E ( 等量代换 )
【解析】由BE//CD 得∠2=∠C,根据是两直线平行,同位角相等;而∠1=∠A得AC∥DE,根据是内错角相等,两直线平行;再根据两直线平行,内错角相等得∠2=∠E,由等量代换 即可得到结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】湖南铁路“五纵五横”的干线网、以长沙为中心的“一环八射”快速网将在2020年初步完成,届时长沙铁路总里程将达到6800公里左右,数据6800用科学记数法表示为( )
A. 0.68×104B. 6.8×103C. 68×102D. 680×101
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在平面直角坐标系xoy中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,与双曲线
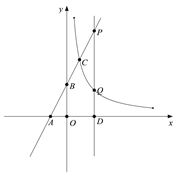
轴分别交于点A、B,与双曲线![]() 在第一象限内交于点C(1,m).
在第一象限内交于点C(1,m).
(1)求![]() 和
和![]() 的值;
的值;
(2)过![]() 轴上的点D(
轴上的点D(![]() ,0)作平行于y轴的直线
,0)作平行于y轴的直线![]() (
(![]() ),分别与直线AB和双曲线
),分别与直线AB和双曲线![]() 交于点P、Q,且PQ=2QD,求△APQ的面积.
交于点P、Q,且PQ=2QD,求△APQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标.
(2)探究下列问题:①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com