
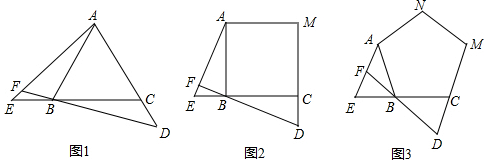
分析 探究:(1)根据△BCA是等边三角形,得出BC=AB,∠ACB=∠ABC=60°,进而得到∠BCD=∠ABE=120°,从而得到△CBD≌△BAE(SAS);(2)利用全等三角形的性质得到对应角相等,再利用三角形的内角和定理,即可得出∠BFE=∠BCD,进而得解;
应用:利用正方形(或正五边形)的性质得到BC=AB,∠BCD=∠ABE,从而判断出△CBD≌△BAE(SAS);再利用全等三角形的性质得到∠CDN=∠BCM,再利用全等三角形的性质得到对应角相等,再利用三角形的内角和定理,即可得出∠BFE=∠BCD,进而得解;
拓展:利用相同的方法可得出全等三角形,再利用全等三角形的性质得到对应角相等,再利用三角形的内角和,即可得出∠BFE的度数为正n边形的外角度数.
解答  探究:(1)解:∵△BCA是等边三角形,
探究:(1)解:∵△BCA是等边三角形,
∴BC=AB,∠ACB=∠ABC=60°,
∴∠BCD=∠ABE=120°,
在△CBD和△BAE中,
$\left\{\begin{array}{l}{BC=AB}\\{∠BCD=∠ABE}\\{CD=BE}\end{array}\right.$,
∴△CBD≌△BAE(SAS);
(2)解:∵△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-60°=120°,
∴∠BFE=120°,
故答案为120;
应用:图2中,根据SAS易证△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-90°=90°,
∴∠BFE=90°,
图3中,根据SAS易证△CBD≌△BAE,
∴∠E=∠D,
∵∠EBF=∠DBC,
∴∠BFE=∠BCD,
又∵∠BCD=180°-108°=72°,
∴∠BFE=72°,
故答案为90°;72°.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE的度数为正n边形的外角度数,
即∠BFE=($\frac{360}{n}$)°,
故答案为:($\frac{360}{n}$)°
点评 本题是四边形的综合题,也是一道规律题,主要考查了正n边形的性质,解题时需要运用等边三角形、正方形、正五边形的性质以及全等三角形的性质和判定,三角形的内角和定理等,解题的关键是利用全等三角形的对应角相等以及三角形内角和定理进行推导,并找出规律.


科目:初中数学 来源: 题型:选择题
| A. | 如果两个三角形全等,则它们一定能关于某直线成轴对称 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形的对称轴是底边上的高 | |
| D. | 若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
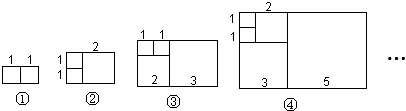
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+2)2+1 | B. | y=2(x-2)2+1 | C. | y=2(x+2)2-1 | D. | y=2(x-2)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com