Question

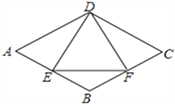
【题目】如图，在菱形ABCD中，E是AB边上一点，且∠A=∠EDF=60°，有下列结论：①AE=BF；②△DEF是等边三角形；③△BEF是等腰三角形；④当AD=4时，△DEF的面积的最小值为.其中结论正确的个数是（　）

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】连接BD，如图所示：

∴AD=AB，∠ADB=∠ADC，AB∥CD，
∵∠A=60°，
∴∠ADC=120°，∠ADB=60°，
同理：∠DBF=60°，
即∠A=∠DBF，
∴△ABD是等边三角形，
∴AD=BD，
∵∠ADE+∠BDE=60°，∠BDE+∠BDF=∠EDF=60°，
∴∠ADE=∠BDF，
∵在△ADE和△BDF中，

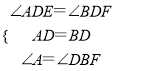
∴△ADE≌△BDF（ASA），
∴DE=DF，AE=BF，故①正确；
∵∠EDF=60°，
∴△DEF是等边三角形，
∴②正确；
∵△ADE≌△BDF，
∴AE=BF，
同理：BE=CF，
但BE不一定等于BF．
故③错误．
∵△DEF是等边三角形，边长最短时，面积最小，
∴当DE⊥AB时，DE最短，此时E为AB的中点，BE=AB=AD=2，

∴DE=2,

∴△DEF的面积=,

∴④正确；
正确的结论有3个.

故选C．