
分析 (1)原价为10元,第一次降价后的价格是10×(1-x)元,第二次降价是在第一次降价后的价格的基础上降价的为:10×(1-x)×(1-x)=10(1-x)2元,则函数解析式即可求得;
(2)求出顶点坐标,画出图象即可;
(3)把x=0.1,代入(1)中函数表达式即可.
解答 解:设平均每次降价的百分率为x,根据题意可得:
y与x之间的函数关系为:y=10(1-x)2.
(2)抛物线的顶点坐标为(1,0),图象如下:
(3)把x=0.1,代入y=10(1-x)2,
y=10×(1-0.1)2=8.1.
两次降价后该药品的价格为8.1元.
点评 此题主要考查了根据实际问题列二次函数关系式,本题需注意第二次降价是在第一次降价后的价格的基础上降价的.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
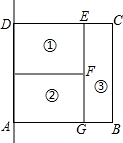 如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?
如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.
如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值/克 | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 4 | 3 | 6 | 3 | 3 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com