
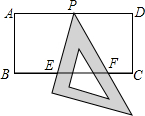
 如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )
如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )| A. | 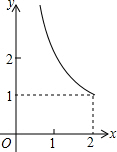 | B. | 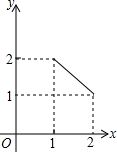 | C. | 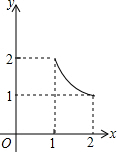 | D. | 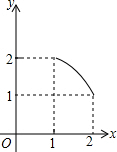 |
分析 连接CP、BP,易证△APB与△DPC是全等的等腰直角三角形,那么△CPB是等腰直角三角形,把△BPE绕点P逆时针旋转90°得到△CPG,根据旋转的性质可得PE=PG,∠PCG=∠PBE=45°,从而得到∠FCG=90°,再求出∠FPG=45°,从而得到∠FPG=∠FPE,然后利用“边角边”证明△PEF和△PGF全等,根据全等三角形对应边相等可得FG=EF,然后表示出BE、CF、EF,再利用勾股定理列式整理得到y与x的函数关系式,最后选择答案即可.
解答 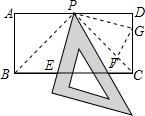 解:如图,连接CP、BP,
解:如图,连接CP、BP,
∵在矩形ABCD中,AD=2,AB=1,P是AD的中点,
∴△APB与△DPC都是等腰直角三角形,且△APB≌△DPC,
∴PB=PC,∠BPC=90°.
把△BPE绕点P逆时针旋转90°得到△CPG,连结FG.
则PE=PG,∠PCG=∠PBE=45°,
∴∠FCG=∠BCP+∠PCG=45°+45°=90°,
∵∠EPF=45°,
∴∠FPG=∠FPE=45°,
在△PEF和△PGF中,
$\left\{\begin{array}{l}{PE=PG}\\{∠FPE=∠FPG}\\{PF=PF}\end{array}\right.$,
∴△PEF≌△PGF(SAS),
∴EF=GF,
∵BC=AD=2,BF=x,CE=y,
∴CG=BE=2-y,CF=2-x,
EF=BC-BE-CF=2-(2-y)-(2-x)=x+y-2,
在Rt△CFG中,CF2+CG2=FG2,
即(2-x)2+(2-y)2=(x+y-2)2,
整理得,y=$\frac{2}{x}$,
纵观各选项,只有C选项图形符合.
故选C.
点评 本题考查了动点问题函数图象,根据点P是AD的中点,作辅助线构造出全等三角形和Rt△CFG是解题的关键,整理得到y与x的函数关系式是本题的难点.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
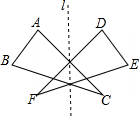 如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.
如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
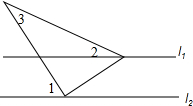 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 26°40′ | B. | 27°20′ | C. | 27°40′ | D. | 73°20′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
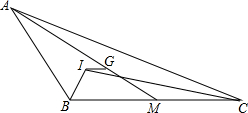 如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.
如图,在△ABC中,∠ABC、∠ACB的平分线交于点I,AM是BC上的中线,G为AM上一点,AG:GM=2:1,IG∥BC.求证:AB+AC=2BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com