
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
(1)求∠BCH的度数;
(2)求证:CE=BH.

【答案】(1)22.5°;(2)见解析.
【解析】试题分析:(1)根据AE是角平分线,可得∠ACE的度数,再根据直角三角形两余角互余可得∠AEC的度数,再由CH⊥AE即可得;
(2)证明CF=CE,再证明△ACF≌△CBH即可得.
试题解析:(1)∵∠ACB=90°,AC=BC,
∴∠CAB=∠B=45°,
∵AE是△ABC的角平分线,
∴∠CAE=![]() ∠CAB=22.5°,
∠CAB=22.5°,
∴∠AEC=90°-∠CAE=67.5°,
∵CH⊥AE于G,
∴∠CGE=90°,
∴∠GCE=90°-∠AEC=22.5°;
(2)∵∠ACB=90°,AC=BC,CD是△ABC的高,
∴∠ACD=![]() ∠ACB=45°,
∠ACB=45°,
∴∠CFE=∠CAE+∠ACD=67.5°,
∴∠CFE=∠AEC,
∴CF=CE,
在△ACF和△CBH中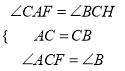 ,∴△ACF≌△CBH,∴CF=BH,
,∴△ACF≌△CBH,∴CF=BH,
∴CE=BH.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,∠B=20°,则∠A4=( )
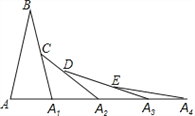
A. 10° B. 15° C. 30° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
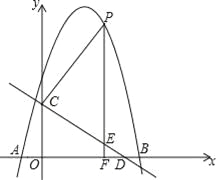
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A. 4![]() B. 6 C. 3
B. 6 C. 3![]() D. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com