
 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12. 分析 求出△ABC和△DBE相似,根据相似三角形面积的比等于相似比的平方求出S△BDE:S△ABC的值,设S△BDE=S,根据等高的三角形的面积的比等于底边的比表示出S△BCD,然后表示出S△ACD,最后求解即可.
解答 解:∵DE∥AC,
∴△ABC∽△DBE,
∴S△BDE:S△ABC=(BE:BC)2,
∵BE:BC=1:4,
∴S△BDE:S△ABC=1:16,
设S△BDE=S,则S△ABC=16S,
∵BE:BC=1:4,
∴S△BCD=4S△BDE=4S,
∴S△ACD=16S-4S=12S,
∴S△BDE:S△ACD=S:12S=1:12.
故答案为:1:12.
点评 本题考查了相似三角形的判定与性质,主要利用了相似三角形的面积的比等于相似比的平方,等高的三角形的面积的比等于底边的比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
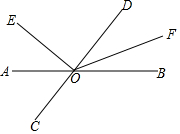 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
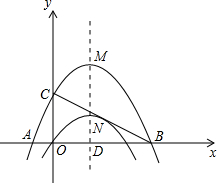 已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.
已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
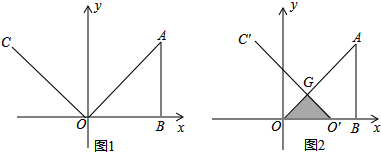
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
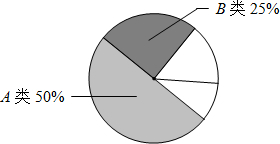 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
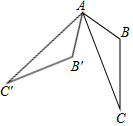 如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为( )
如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为( )| A. | 33° | B. | 50° | C. | 17° | D. | 27° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com