
【题目】在![]() 是斜边
是斜边![]() 上的中线,将
上的中线,将![]() 沿直线CM 折叠,点 A 落在点 D 处,如果CD 恰好与 AB 垂直,那么∠A 等于________度.
沿直线CM 折叠,点 A 落在点 D 处,如果CD 恰好与 AB 垂直,那么∠A 等于________度.
【答案】30
【解析】
先根据折叠的性质得∠1=∠2,由CM为直角△ABC斜边上的中线,根据直角三角形斜边上的中线性质得MA=MC=MB,则∠1=∠A,根据三角形外角性质得∠3=∠1+∠A=2∠1=2∠2,再由CD⊥AB得到∠3+∠2=90°,根据三角形内角和定理可计算出∠2=30°,即可得到结果.
解:如图,
∵△ABC的中线CM将△CMA折叠,使点A落在点D处,
∴∠1=∠2,
∵CM为直角△ABC斜边上的中线,
∴MA=MC=MB,
∴∠1=∠A,
∴∠2=∠A,∠3=∠1+∠A=2∠1=2∠2,
∵CD⊥AB,
∴∠3+∠2=90°,
∴2∠2+∠2=90°,
∴∠2=30°,
∴∠A=30°.
故答案为:30.



科目:初中数学 来源: 题型:
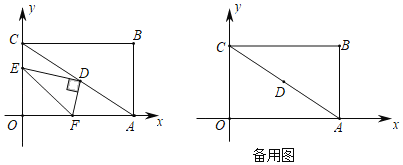
【题目】如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.
(1)当t的值为 时,四边形DEOF是矩形;
(2)用含t的代数式表示线段OF的长度,并说明理由;
(3)当△OEF面积为![]() 时,请直接写出直线DE的解析式.
时,请直接写出直线DE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①4a﹣2b+c>0;②3a+b>0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个互异实根.其中正确结论的个数是( )
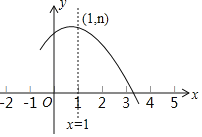
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
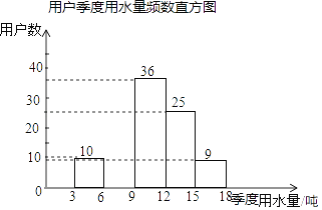
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个被等分成4个扇形的圆形转盘,其中3个扇形分别标有数字2,5,6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).

(1)求当转动这个转盘,转盘自由停止后,指针指向没有标数字
的扇形的概率;
(2)请在4,7,8,9这4个数字中选出一个数字填写在没有标数字的扇形内,使得分别转动转盘2次,转盘自由停止后指针所指扇形的数字和分别为奇数与为偶数的概率相等,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com