
【题目】若顺次连接四边形ABCD各边中点所得的四边形是矩形,则下列结论中正确的是( )
A.AB∥CDB.AB⊥BCC.AC=BDD.AC⊥BD
【答案】D
【解析】
这个四边形ABCD的对角线AC和BD的关系是互相垂直.理由为:根据题意画出相应的图形,如图所示,由四边形EFGH为矩形,根据矩形的四个角为直角得到∠FEH=90°,又EF为三角形ABD的中位线,根据中位线定理得到EF与DB平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到EH与AC平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到AC与BD垂直.
如图:
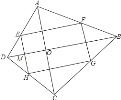
∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故选:D.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
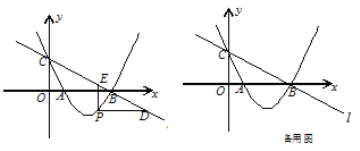
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
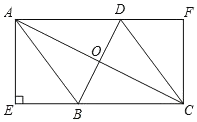
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=8,AD=10,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2015年市政府共投资3亿元人民币建设了廉租房12万平方米,2017年计划投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,问从2015到2017年这三年共建设了多少万平方米廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A (1,3),这两条直线分别与x轴交于B,C两点.
交于点A (1,3),这两条直线分别与x轴交于B,C两点.
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数据是甲、乙、丙三人各10轮投篮的得分(每轮投篮10次,每次投中记1分):
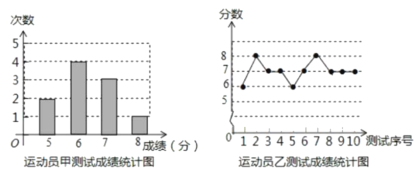
丙得分的平均数与众数都是7,得分统计表如下:
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力,你认为选谁更合适?请用你所学过的统计知识加以分析说明(参考数据:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之间进行传球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,经过三次传球后球又回到乙手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中每个小方格都是边长为1个单位长度的正方形,![]() 在方格纸中的位置如图所示.
在方格纸中的位置如图所示.

(1)请在图中建立平面直角坐标系,使得![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,并写出
,并写出![]() 点的坐标;
点的坐标;
(2)在图中作出![]() 绕坐标原点旋转
绕坐标原点旋转![]() 后的
后的![]() ,并写出
,并写出![]() ,
,![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com