
【题目】下列数据是甲、乙、丙三人各10轮投篮的得分(每轮投篮10次,每次投中记1分):
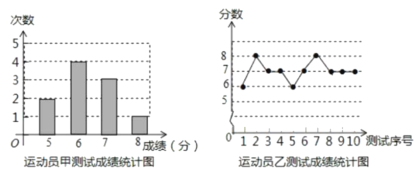
丙得分的平均数与众数都是7,得分统计表如下:
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力,你认为选谁更合适?请用你所学过的统计知识加以分析说明(参考数据:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之间进行传球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,经过三次传球后球又回到乙手中的概率是多少?(用树状图或列表法解答)
【答案】(1)7,7;(2)选择乙更合适,理由是:在平均数相同的情况下,选择方差小的,因为方差越小,表示得分越稳定;(3)经过三次传球后球又回到乙手中的概率为![]() .
.
【解析】
(1)根据平均数的计算公式、众数的定义即可得;
(2)先计算出甲、乙的平均数,再利用平均数与方差的意义进行决策即可;
(3)先画出树状图,再找出事件的所有可能的结果,然后找出经过三次传球后球又回到乙手中的结果,最后利用概率公式计算即可得.
(1)![]() 丙得分的众数是7
丙得分的众数是7
![]() a和b中至少有一个等于7
a和b中至少有一个等于7
由平均数的公式得:![]()
整理得:![]()
则![]() ,
,![]()
故答案为:7,7;
(2)由图可知,甲10轮投篮的得分依次为![]()
乙10轮投篮的得分依次为![]()
则甲得分的平均数为![]()
乙得分的平均数为![]()
又因为![]() ,即
,即![]()
所以由平均数可知,应该选择乙、丙;由方差可知,选择乙更合适,理由是方差越小,表示得分越稳定
答:选择乙更合适,理由是:在平均数相同的情况下,选择方差小的,因为方差越小,表示得分越稳定;
(3)依题意,画树状图如下:

由此可知,经过三次传球的所有可能的结果共有8种,它们每一种出现的可能性都相等,其中,经过三次传球后球又回到乙手中的结果有2种
则所求的概率为![]()
答:经过三次传球后球又回到乙手中的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点A,B的坐标分别为(1,0),(0,2),AC⊥AB,且AB=AC,直线BC交![]() 轴于点D,抛物线
轴于点D,抛物线![]() 经过点A,B,D.
经过点A,B,D.

(1)求直线BC和抛物线![]() 的函数表达式;
的函数表达式;
(2)点P是直线BD下方的抛物线上一点,求△PCD面积的最大值,以及△PCD面积取得最大值时,点P的坐标;
(3)若点P的坐标为(2)小题中,△PCD的面积取得最大值时对应的坐标.平面内存在直线l,使点B,D,P到该直线的距离都相等,请直接写出所有满足条件的直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在疫情期间购进一批含75%酒精的消毒湿巾投放市场,则开始,由于消费者对此类产品认识不足,前几天的销量每况愈下;为了打开市场,提高销量,超市决定对该消毒湿巾打折销售,日销量每日增加,时间每增加1天,则日销量增加20包.超市工作人员对一个月(30天)销售情况进行了跟踪记录,并将记录情况绘成图像,图中的折线ABC表示该消毒湿巾日销量y(包)与销售时间x(天)之间的函数关系;
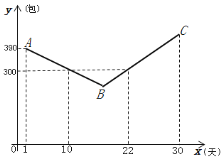
(1)第28天的日销售量是_______包;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)若该产口进价为5元/包,AB段售价为15元/包,BC段在15元/包的基础上打a折销售,并且在30天中利润不低于3400元的天数有且只有10天,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①4a﹣2b+c>0;②3a+b>0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个互异实根.其中正确结论的个数是( )
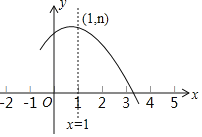
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
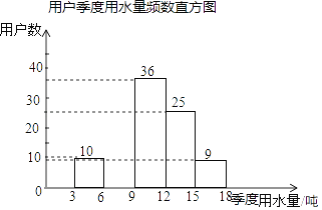
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
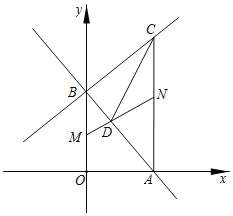
【题目】如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A(5,0),与y轴交于点B;直线y═![]() x+6过点B和点C,且AC⊥x轴.点M从点B出发以每秒2个单位长度的速度沿y轴向点O运动,同时点N从点A出发以每秒3个单位长度的速度沿射线AC向点C运动,当点M到达点O时,点M、N同时停止运动,设点M运动的时间为t(秒),连接MN.
x+6过点B和点C,且AC⊥x轴.点M从点B出发以每秒2个单位长度的速度沿y轴向点O运动,同时点N从点A出发以每秒3个单位长度的速度沿射线AC向点C运动,当点M到达点O时,点M、N同时停止运动,设点M运动的时间为t(秒),连接MN.
(1)求直线y=kx+b的函数表达式及点C的坐标;
(2)当MN∥x轴时,求t的值;
(3)MN与AB交于点D,连接CD,在点M、N运动过程中,线段CD的长度是否变化?如果变化,请直接写出线段CD长度变化的范围;如果不变化,请直接写出线段CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com